Question

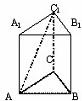
如图，正三棱柱A-BCD中，E在棱AB上，F在棱CD上，并使AE：EB=CF：FD=m（m＞0），设α为异面直线EF和AC所成的角，β为异面直线EF和BD所成的角，则α+β的值是

π

2

．

Answer 1

分析：要求α+β的值，关键是作出异面直线的所成角，利用比例关系，寻找平行线，从而得到线线角．

解答：解：过点F作BD的平行线，交BC于M，则
∵AE：EB=CF：FD=m，∴EM∥AC
∴α=∠MEF，β=∠MFE
∵正三棱柱A-BCD，∴AC⊥BD
∴α+β=

π

2

故答案为

π

2

点评：本题的考点是异面直线及其所成的角，主要考查异面直线及其所成的角的寻找与求解，关键是作出异面直线所成的角，同等考查了正棱锥的性质．