题目内容
用数字0,1,2,3组成数字可以重复的四位数,其中有且只有一个数字出现两次的四位数的个数为( )
| A.144 | B.120 | C.108 | D.72 |
C
解析试题分析:用数字0,1,2,3组成数字可以重复的四位数,
① 如果重复数字为0,
则需要从1,2,3中再选取两个不同的数字,且0不能放在首位,
故首位应从两个非零数字中选择一个,而另一个非零数字可从剩余的三个数位中选择一位进行放置,则共有: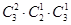 =3×2×3=18个;
=3×2×3=18个;
② 如果重复数字不为0,但抽取的数字含0,
则需要从1,2,3中先选取一个数字重复,再选取一个不重复,从后三位中选择一位放置0,再从剩余的三位中选择一位放置非重复数字,
故有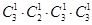 =54种;
=54种;
③ 如果重复数字不为0,但抽取的数字不含0,
则需要从1,2,3中先选取一个数字用做重复,再选取两个用做不重复放置时,应先从四位中先后选择二位放置非重复数字,故有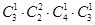 =36种;
=36种;
故有且只有一个数字出现两次的四位数的个数为108个,故选C.
考点:简单排列组合应用问题,计数原理。
点评:中档题,对于含有特殊元素、特殊位置问题,往往从“特殊”入手,分类讨论。本题解答紧紧抓住“0”这个特殊元素,进行讨论。

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
设三位数 ,若以
,若以 为三条边的长可以构成一个等腰(含等边)三角形,则这样的三位数
为三条边的长可以构成一个等腰(含等边)三角形,则这样的三位数 有( )
有( )
| A.12种 | B.24种 | C.28种 | D.36种 |
一个盒子里有3个分别标有号码为1,2,3的小球,每次取出一个,记下它的标号后再放回盒子中,共取3次,则取得小球标号最大值是3的取法有( )
| A.12种 | B.15种 | C.17种 | D.19种 |
若 =
= +
+ +
+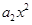 +…+
+…+ (x∈R),则
(x∈R),则 +
+ +
+ +…+
+…+ ( )
( )
A.- | B. | C.- | D. |
二项式 的展开式中常数项为( )
的展开式中常数项为( )
| A.5 | B.10 | C. | D.40 |
二项式(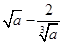 )30的展开式的常数项为第几项
)30的展开式的常数项为第几项
| A.17 | B.18 | C.19 | D.20 |
某市有7条南北向街道,5条东西向街道.图中共有m个矩形,从A点走到B点最短路线的走法有n种,则m,n的值分别为( )
| A.m=90,n=210 | B.m="210,n=210" |
| C.m=210,n=792 | D.m=90,n=792 |
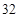

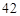

 的二项展开式中x7项的系数为﹣10,则a= .
的二项展开式中x7项的系数为﹣10,则a= .