题目内容
某市有7条南北向街道,5条东西向街道.图中共有m个矩形,从A点走到B点最短路线的走法有n种,则m,n的值分别为( )
| A.m=90,n=210 | B.m="210,n=210" |
| C.m=210,n=792 | D.m=90,n=792 |
B
解析试题分析:每个矩形需要两条横向、两条纵向的线段,所以,图中共有矩形m= 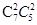 =210个;
=210个;
每条东西向的街道被分成6段,每条南北向的街道被分成4段.从A到B最短的走法,无论怎样走,一定包括10段,其中6段相同方向,另4段也相同方向.从而,不同的走法有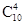 =
=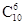 =210,故选B。
=210,故选B。
考点:简单的组合应用问题。
点评:中档题,注意将问题转化成简单组合问题,利用组合数公式求解。

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
用数字0,1,2,3组成数字可以重复的四位数,其中有且只有一个数字出现两次的四位数的个数为( )
| A.144 | B.120 | C.108 | D.72 |
从5位男教师和4位女教师中选出3位教师,派到3个班担任班主任(每班1位班主任),要求这3位班主任中男、女教师都要有,则不同的选派方案共有:
| A.210种 | B.420种 | C.630种 | D.840种 |
记者要为5名志愿者和他们帮助的2位老人拍照,要求排成一排,2位老人相邻但不排在两端,不同的排法共有( )
| A.1440种 | B.960种 | C.720种 | D.480种 |
某单位安排2013年春节期间7天假期的值班情况,7个员工每人各值一天. 已知某员工甲必须排在前两天,员工乙不能排在第一天,员工丙必须排在最后一天,则不同的值班顺序有( )
| A.120种 | B.216种 | C.720种 | D.540种 |
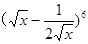 的展开式中常数项为
的展开式中常数项为
A.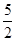 | B.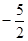 | C.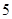 | D.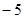 |
若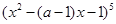 的展开式中没有x的奇次幂项,则含
的展开式中没有x的奇次幂项,则含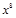 项的系数为( )
项的系数为( )
| A.5 | B.-5 | C.10 | D.-10 |
使得 ( )
( )
A.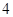 | B.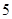 | C.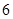 | D.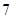 |