题目内容
是否存在实数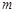 ,使得
,使得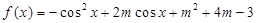 的最大值为
的最大值为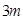 ,若存在,求出
,若存在,求出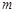 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
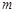 ,使得
,使得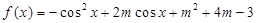 的最大值为
的最大值为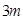 ,若存在,求出
,若存在,求出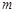 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.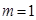 或
或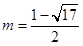
试题分析:由题设可假定存在,若能说明其成立则进而可求得其值,若能推出矛盾则说明其不存在.
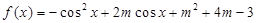
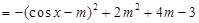 ,结合
,结合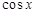 的取值范围,分类讨论
的取值范围,分类讨论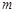 的取值范围,从而使得问题迎刃解决.分三种情况来讨论:ⅰ)当
的取值范围,从而使得问题迎刃解决.分三种情况来讨论:ⅰ)当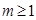 时;ⅱ)当
时;ⅱ)当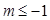 时;ⅲ)当
时;ⅲ)当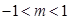 时.
时.试题解析:
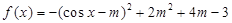
假设存在满足条件的
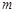 .
.ⅰ)当
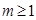 时,
时,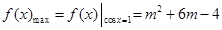
令
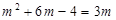 ,得
,得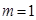 (
(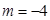 舍去)
舍去)ⅱ)当
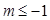 时,
时,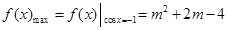
令
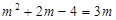 ,得
,得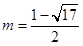 (
(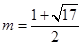 舍去)
舍去)ⅲ)当
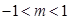 时,
时,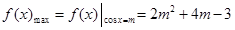
令
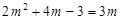 ,得
,得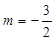 (舍去)
(舍去)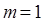 (舍去)
(舍去)综上,存在
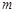 使得
使得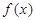 的最大值为
的最大值为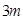 .
.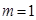 或
或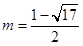

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
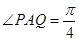 (其中点P、Q分别在边BC、CD上),搜索区域为平面四边形APCQ围成的海平面.设
(其中点P、Q分别在边BC、CD上),搜索区域为平面四边形APCQ围成的海平面.设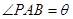 ,搜索区域的面积为
,搜索区域的面积为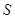 .
.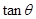 的关系式,并指出
的关系式,并指出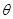 的取值范围;
的取值范围;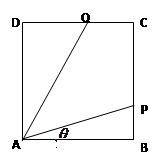
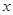 公里的相邻两增压站之间的输油管道费用为
公里的相邻两增压站之间的输油管道费用为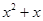 万元.设余下工程的总费用为
万元.设余下工程的总费用为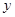 万元.
万元.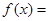
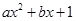 ,(1) 若
,(1) 若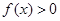 的解集是
的解集是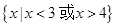 ,求实数
,求实数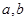 的值;(2) 若
的值;(2) 若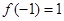 且
且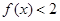 恒成立,求实数
恒成立,求实数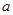 的取值范围.
的取值范围.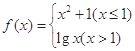 ,则
,则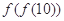 = .
= .