题目内容
(2012•盐城一模)已知矩阵A=
,B=
,若矩阵AB对应的变换把直线l:x+y-2=0变为直线l',求直线l'的方程.
|
|
分析:先计算矩阵AB对应的变换,再求出在变换下点的坐标之间的对应关系,从而可求直线l'的方程.
解答:解:∵A=
,B=
,
∴AB=
=
…(3分),
在直线l上任取一点P(x′,y′),经矩阵AB变换为点Q(x,y),则
=
=
,
∴
,
即
…(8分)
代入x′+y′-2=0中得x-
y+
-2=0,
∴直线l′的方程为4x+y-8=0…(10分)
|
|
∴AB=
|
|
|
在直线l上任取一点P(x′,y′),经矩阵AB变换为点Q(x,y),则
|
|
|
|
∴
|
即
|
代入x′+y′-2=0中得x-
| 1 |
| 4 |
| y |
| 2 |
∴直线l′的方程为4x+y-8=0…(10分)
点评:本题重点考查矩阵变换,考查矩阵变换的运用,解题的关键是求出矩阵AB对应的变换

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
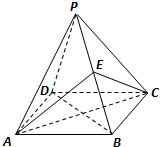 (2012•盐城一模)如图,在四棱锥P-ABCD中,四边形ABCD是菱形,PA=PC,E为PB的中点.
(2012•盐城一模)如图,在四棱锥P-ABCD中,四边形ABCD是菱形,PA=PC,E为PB的中点.