题目内容
已知抛物线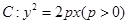 的焦点
的焦点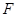 到准线的距离为
到准线的距离为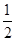 .过点
.过点
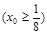
作直线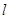 交抛物线
交抛物线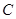 与
与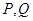 两点(
两点( 在第一象限内).
在第一象限内).
(1)若 与焦点
与焦点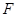 重合,且
重合,且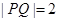 .求直线
.求直线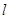 的方程;
的方程;
(2)设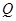 关于
关于 轴的对称点为
轴的对称点为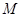 .直线
.直线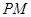 交
交 轴于
轴于 . 且
. 且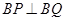 .求点
.求点 到直线
到直线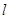 的距离的取值范围.
的距离的取值范围.
(1) 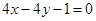 或
或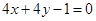 ;(2)
;(2) 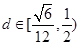
解析试题分析:(1) 首先求出抛物线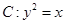 再与
再与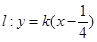 联立得到关于x的一元二次方程,最后利用焦半径公式求出斜率即可.(2)先求出
联立得到关于x的一元二次方程,最后利用焦半径公式求出斜率即可.(2)先求出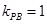 ,进而转换为
,进而转换为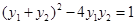 ,再由l与C联立得
,再由l与C联立得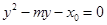 ,借助于根与系数的关系求出m的取值范围,然后由点到直线的距离公式得到d的表达式,最后根据基本不等式求出范围.
,借助于根与系数的关系求出m的取值范围,然后由点到直线的距离公式得到d的表达式,最后根据基本不等式求出范围.
由题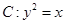
(1)A与下重合,则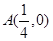 设
设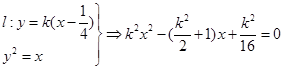
又由焦半径公式有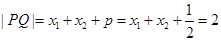
可求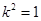 ∴
∴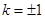 .
.
所求直线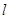 为:
为: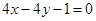 或
或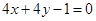
(2)可求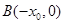 .故△BQM为等腰直角三角形,设
.故△BQM为等腰直角三角形,设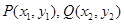
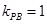 . 即
. 即 .
.
设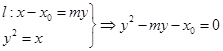 ∴
∴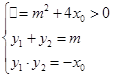
从而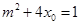 , 即
, 即 , 又
, 又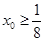 .
.
∴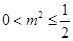 .
.
点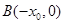 到直线
到直线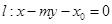 的距离为
的距离为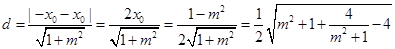
∴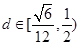
考点:抛物线的性质;焦半径公式;根与系数的关系;点到直线的距离公式;基本不等式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
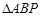 的三个顶点在抛物线
的三个顶点在抛物线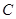 :
: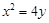 上,
上,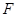 为抛物线
为抛物线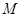 为
为 的中点,
的中点,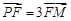 ;
;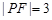 ,求点
,求点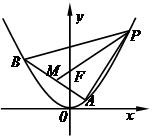
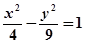 ,F1,F2是其两个焦点,点M在双曲线上.
,F1,F2是其两个焦点,点M在双曲线上.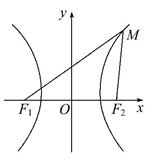
 :
: .
.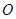 为原点,若点
为原点,若点 在椭圆
在椭圆 在直线
在直线 上,且
上,且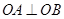 ,试判断直线
,试判断直线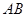 与圆
与圆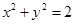 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.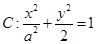
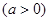 的焦点在x轴上,左右顶点分别为
的焦点在x轴上,左右顶点分别为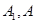 ,上顶点为B,抛物线
,上顶点为B,抛物线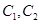 分别以A,B为焦点,其顶点均为坐标原点O,
分别以A,B为焦点,其顶点均为坐标原点O,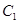 与
与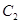 相交于 直线
相交于 直线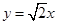 上一点P.
上一点P.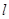 与直线OP垂直,且与椭圆C交于不同的两点M,N,已知点
与直线OP垂直,且与椭圆C交于不同的两点M,N,已知点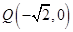 ,求
,求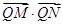 的最小值。
的最小值。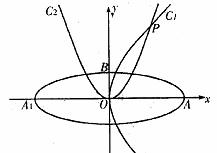
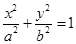 上的点M与椭圆右焦点
上的点M与椭圆右焦点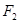 的连线
的连线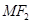 与x轴垂直,且OM(O是坐标原点)与椭圆长轴和短轴端点的连线AB平行.
与x轴垂直,且OM(O是坐标原点)与椭圆长轴和短轴端点的连线AB平行.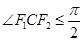 ;
;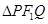 的面积是20
的面积是20 ,求此时椭圆的方程.
,求此时椭圆的方程.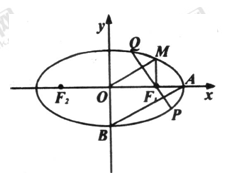
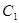 的圆心在坐标原点
的圆心在坐标原点 ,且恰好与直线
,且恰好与直线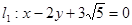 相切,设点A为圆上一动点,
相切,设点A为圆上一动点,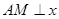 轴于点
轴于点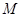 ,且动点
,且动点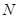 满足
满足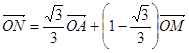 ,设动点
,设动点
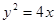 的顶点作射线
的顶点作射线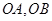 与抛物线交于
与抛物线交于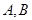 ,若
,若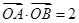 ,求证:直线
,求证:直线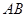 过定点.
过定点.