题目内容
过抛物线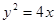 的顶点作射线
的顶点作射线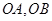 与抛物线交于
与抛物线交于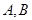 ,若
,若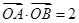 ,求证:直线
,求证:直线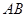 过定点.
过定点.
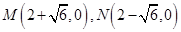 .
.
解析试题分析:设直线AB的方程为: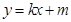 ,
,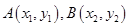 ,联立可得
,联立可得 得
得 ,根据
,根据 和韦达定理可求出
和韦达定理可求出 得
得 ,即可求出直线AB的方程:
,即可求出直线AB的方程: 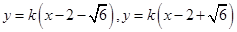 ,即可得到直线AB的定点.
,即可得到直线AB的定点.
解 : 设 ,
,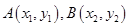
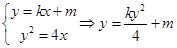 ,即 :
,即 : 
 (1)
(1)
即: 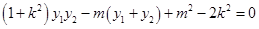 (2)
(2)
将(1)代入(2) 

直线AB的方程: 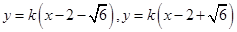
所以直线AB过定点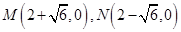
考点:1.直线方程;2.直线与抛物线的位置关系.

练习册系列答案
相关题目
题目内容
过抛物线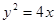 的顶点作射线
的顶点作射线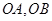 与抛物线交于
与抛物线交于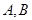 ,若
,若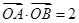 ,求证:直线
,求证:直线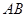 过定点.
过定点.
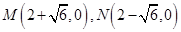 .
.
解析试题分析:设直线AB的方程为: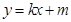 ,
,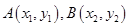 ,联立可得
,联立可得 得
得 ,根据
,根据 和韦达定理可求出
和韦达定理可求出 得
得 ,即可求出直线AB的方程:
,即可求出直线AB的方程: 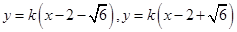 ,即可得到直线AB的定点.
,即可得到直线AB的定点.
解 : 设 ,
,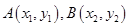
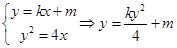 ,即 :
,即 : 
 (1)
(1)
即: 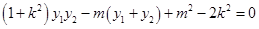 (2)
(2)
将(1)代入(2) 

直线AB的方程: 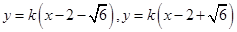
所以直线AB过定点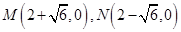
考点:1.直线方程;2.直线与抛物线的位置关系.
