题目内容
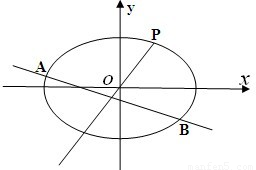
如图,在平面内直线EF与线段AB相交于C点,∠BCF=30°,且AC=CB=4,将此平面沿直线EF折成60°的二面角α-EF-β,BP⊥平面α,点P为垂足.
(Ⅰ) 求△ACP的面积;
(Ⅱ) 求异面直线AB与EF所成角的正切值.
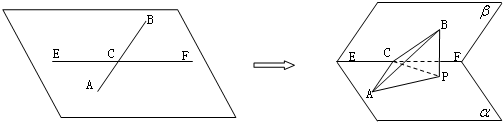
分析:(I)在平面α内,过点P作PM⊥EF,点M为垂足,连接BM,则∠BMP为二面角α-EF-β的平面角,由已知中二面角α-EF-β的平面角为60°,结合,∠BCF=30°,且AC=CB=4,求出CP长及sin∠ACP,代入三角形面积公式,即可得到△ACP的面积;
(Ⅱ)过点A作AQ∥EF,交MP于点Q,则∠BAQ是AB与EF所成的角,且AQ⊥平面BMQ,解三角形△BAQ即可得到AB与EF所成角的正切值.
(Ⅱ)过点A作AQ∥EF,交MP于点Q,则∠BAQ是AB与EF所成的角,且AQ⊥平面BMQ,解三角形△BAQ即可得到AB与EF所成角的正切值.
解答: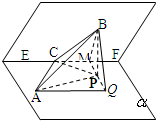 解:(Ⅰ) 如图,在平面α内,过点P作PM⊥EF,点M为垂足,
解:(Ⅰ) 如图,在平面α内,过点P作PM⊥EF,点M为垂足,
连接BM,则∠BMP为二面角α-EF-β的平面角.
在Rt△BMC中,由∠BCM=30°,CB=4,得CM=2
,BM=2.
在Rt△BMP中,由∠BMP=60°,BM=2,得MP=1.在Rt△CMP中,
由CM=2
,MP=1,得CP=
,cos∠PCM=
,sin∠PCM=
.
故 sin∠ACP=sin(150°-∠PCM)=
.所以S△ACP=3
.…(7分)
(Ⅱ) 如图,过点A作AQ∥EF,交MP于点Q,
则∠BAQ是AB与EF所成的角,且AQ⊥平面BMQ.
在△BMQ中,由∠BMQ=60°,BM=MQ=2,得BQ=2.…(10分)
在Rt△BAQ中,由AQ=AC•cos30°+CM=4
,BQ=2,得tan∠BAQ=
=
.
因此AB与EF所成角的正切值为
.…(13分)
 解:(Ⅰ) 如图,在平面α内,过点P作PM⊥EF,点M为垂足,
解:(Ⅰ) 如图,在平面α内,过点P作PM⊥EF,点M为垂足,连接BM,则∠BMP为二面角α-EF-β的平面角.
在Rt△BMC中,由∠BCM=30°,CB=4,得CM=2
| 3 |
在Rt△BMP中,由∠BMP=60°,BM=2,得MP=1.在Rt△CMP中,
由CM=2
| 3 |
| 13 |
2
| ||
|
| 1 | ||
|
故 sin∠ACP=sin(150°-∠PCM)=
3
| ||
2
|
| 3 |
(Ⅱ) 如图,过点A作AQ∥EF,交MP于点Q,
则∠BAQ是AB与EF所成的角,且AQ⊥平面BMQ.
在△BMQ中,由∠BMQ=60°,BM=MQ=2,得BQ=2.…(10分)
在Rt△BAQ中,由AQ=AC•cos30°+CM=4
| 3 |
| BQ |
| AQ |
| ||
| 6 |
因此AB与EF所成角的正切值为
| ||
| 6 |
点评:本题考查的知识点是与二面角有关的立体几何综合题,其中(I)的关键是构造出∠BMP为二面角α-EF-β的平面角,进而解三角形求出CP长及sin∠ACP,(II)的关键是构造出∠BAQ是AB与EF所成的角.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
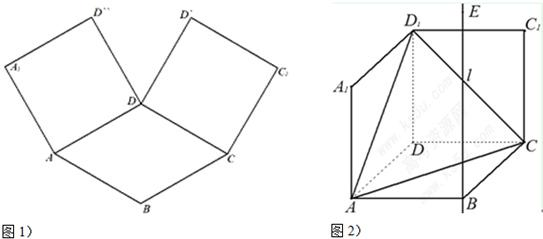
 如图,在平面直坐标系xOy中,已知椭圆
如图,在平面直坐标系xOy中,已知椭圆 中,已知椭圆
中,已知椭圆 ,经过点
,经过点 ,其中e为椭圆的离心率.且椭圆
,其中e为椭圆的离心率.且椭圆 与直线
与直线 有且只有一个交点。
有且只有一个交点。
 与椭圆
与椭圆 在椭圆上,直线
在椭圆上,直线 平分线段
平分线段 ,求:当
,求:当 的面积取得最大值时直线
的面积取得最大值时直线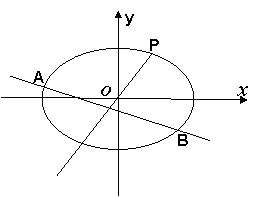
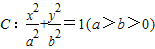 ,经过点(1,e),其中e为椭圆的离心率.且椭圆C与直线
,经过点(1,e),其中e为椭圆的离心率.且椭圆C与直线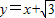 有且只有一个交点.
有且只有一个交点.