题目内容
(本题满分12分)如图,在平面直坐标系 中,已知椭圆
中,已知椭圆 ,经过点
,经过点 ,其中e为椭圆的离心率.且椭圆
,其中e为椭圆的离心率.且椭圆 与直线
与直线 有且只有一个交点。
有且只有一个交点。

(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设不经过原点的直线 与椭圆
与椭圆 相交与A,B两点,第一象限内的点
相交与A,B两点,第一象限内的点 在椭圆上,直线
在椭圆上,直线 平分线段
平分线段 ,求:当
,求:当 的面积取得最大值时直线
的面积取得最大值时直线 的方程。
的方程。
【答案】
(Ⅰ) ;(Ⅱ)
;(Ⅱ)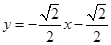 。
。
【解析】
试题分析:(Ⅰ)∵椭圆经过点 ,∴
,∴ 又
又 ,
,
∴ ,∴
,∴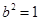
∴椭圆的方程为 …………………………………………2分
…………………………………………2分
又∵椭圆 与直线
与直线 有且只有一个交点
有且只有一个交点
∴方程 即
即 有相等实根
有相等实根
∴ ∴
∴
∴椭圆的方程为 ………………………………………………5分
………………………………………………5分
(Ⅱ)由(Ⅰ)知椭圆的方程为 故
故
设不经过原点的直线 的方程
的方程 交椭圆
交椭圆 于
于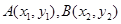
由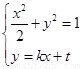 得
得 ……………………………6分
……………………………6分
∴ ………………7分
………………7分

直线 方程为
方程为 且
且 平分线段
平分线段
∴ =
=
 解得
解得  ……………………………………………8分
……………………………………………8分
∴
又∵点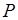 到直线
到直线 的距离
的距离
∴ …………………………………………9分
…………………………………………9分
设
由直线 与椭圆
与椭圆 相交于A,B两点可得
相交于A,B两点可得
求导可得

 ,此时
,此时 取得最大值
取得最大值
此时直线 的方程
的方程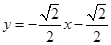 ……………………………………………12分
……………………………………………12分
考点:本题主要考查椭圆标准方程,椭圆的几何性质,直线与椭圆的位置关系,直线方程,点到直线的距离。
点评:求椭圆的标准方程是解析几何的基本问题,涉及直线与椭圆的位置关系问题,常常运用韦达定理,本题属于中档题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 为底面的直棱柱被平面
为底面的直棱柱被平面 所截而得.
所截而得.  ,
, 为
为 的中点.
的中点.
 时,求平面
时,求平面 为何值时,在棱
为何值时,在棱 上存在点
上存在点 ,使
,使 平面
平面 中,已知上下两底面为正方形,且边长均为1;侧棱
中,已知上下两底面为正方形,且边长均为1;侧棱 ,为
,为 中点,
中点, 为
为 中点,
中点, 为
为 上一个动点.
上一个动点.
 ;
; 的平
的平
 中,已知
中,已知 的直径
的直径 的中点.
的中点.
 所成角的正弦值.
所成角的正弦值.
