题目内容
已知O为坐标原点,点A(1,-1),若点M(x,y)为平面区域 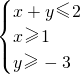 内的一个动点,则
内的一个动点,则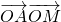 的最大值与最小值之差为________.
的最大值与最小值之差为________.
8
分析:根据向量数量积的坐标公式,得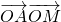 =x-y,目标函数z=x-y对应直线l,在直线l扫过区域的情况下将它进行平移,不难求出z的最大值为8,最小值为0,从而得到本题的答案.
=x-y,目标函数z=x-y对应直线l,在直线l扫过区域的情况下将它进行平移,不难求出z的最大值为8,最小值为0,从而得到本题的答案.
解答: 解:作出不等式组
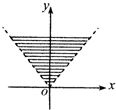
解:作出不等式组 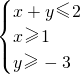 对应的平面区域,如图中阴影部分三角形
对应的平面区域,如图中阴影部分三角形
∵点A(1,-1),M(x,y),
∴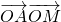 =1×x+(-1)×y=x-y
=1×x+(-1)×y=x-y
将直线l:z=x-y进行平移,可得当l经过点A(1,1)时,x-y有最小值0,
当l经过点B(5,-3)时,x-y有最大值8,
因此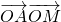 的最大值是8,最小值小值是0,它们的差是8
的最大值是8,最小值小值是0,它们的差是8
故答案为:8
点评:本题给出平面区域内的两个点A、M,求数量积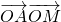 的最大值与最小值之差,着重考查了平面向量数量积的坐标运算和简单的线性规划等知识,属于基础题.
的最大值与最小值之差,着重考查了平面向量数量积的坐标运算和简单的线性规划等知识,属于基础题.
分析:根据向量数量积的坐标公式,得
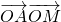 =x-y,目标函数z=x-y对应直线l,在直线l扫过区域的情况下将它进行平移,不难求出z的最大值为8,最小值为0,从而得到本题的答案.
=x-y,目标函数z=x-y对应直线l,在直线l扫过区域的情况下将它进行平移,不难求出z的最大值为8,最小值为0,从而得到本题的答案.解答:
 解:作出不等式组
解:作出不等式组 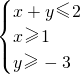 对应的平面区域,如图中阴影部分三角形
对应的平面区域,如图中阴影部分三角形∵点A(1,-1),M(x,y),
∴
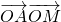 =1×x+(-1)×y=x-y
=1×x+(-1)×y=x-y将直线l:z=x-y进行平移,可得当l经过点A(1,1)时,x-y有最小值0,
当l经过点B(5,-3)时,x-y有最大值8,
因此
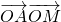 的最大值是8,最小值小值是0,它们的差是8
的最大值是8,最小值小值是0,它们的差是8故答案为:8
点评:本题给出平面区域内的两个点A、M,求数量积
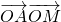 的最大值与最小值之差,着重考查了平面向量数量积的坐标运算和简单的线性规划等知识,属于基础题.
的最大值与最小值之差,着重考查了平面向量数量积的坐标运算和简单的线性规划等知识,属于基础题. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目