题目内容
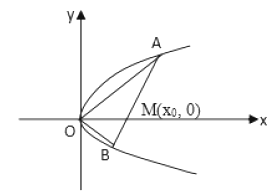
【题目】如图所示,直线 ![]() 与抛物线
与抛物线 ![]() 交于
交于 ![]() 两点,与
两点,与 ![]() 轴交于点
轴交于点 ![]() ,且
,且 ![]() ,
,
(1)求证:点 ![]() 的坐标为
的坐标为 ![]() ;
;
(2)求证: ![]() ;
;
(3)求 ![]() 面积的最小值.
面积的最小值.
【答案】
(1)证明:设 ![]() ,直线
,直线 ![]() 方程为
方程为 ![]() 代入
代入 ![]() 得
得 ![]() ,
, ![]() 是此方程的两根
是此方程的两根![]() ①即
①即 ![]() 点坐标是
点坐标是 ![]()
(2)证明: ![]()
![]() ,则
,则 ![]()
(3)解:由方程①得 ![]() ,又
,又 ![]()
![]()
![]() 当
当 ![]() 时,
时, ![]() 取最小值1.
取最小值1.
【解析】(1)根据y1y2=-1,先设出直线l的方程,联立抛物线,消去x,利用韦达定理得到y1y2=-x0 , 对应可得M点坐标。
(2)用向量证明垂直,如果OA⊥OB,则x1x2+y1y2=0,根据上题可以求得x1x2的值,代入计算即可。
(3)根据已知条件设出三角形的面积公式,利用完全平方和公式转化再代值,最后直接判断根号的最小值。

练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
【题目】某种商品在30天内每克的销售价格![]() (元)与时间
(元)与时间![]() 的函数图像是如图所示的两条线段
的函数图像是如图所示的两条线段![]() ,
,![]() (不包含
(不包含![]() ,
,![]() 两点);该商品在 30 天内日销售量
两点);该商品在 30 天内日销售量![]() (克)与时间
(克)与时间![]() (天)之间的函数关系如下表所示.
(天)之间的函数关系如下表所示.
第 | 5 | 1 5 | 2 0 | 3 0 |
销售量 | 3 5 | 2 5 | 2 0 | 1 0 |
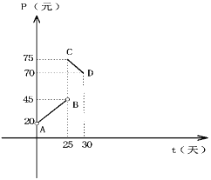
(1)根据提供的图象,写出该商品每克销售的价格![]() (元)与时间
(元)与时间![]() 的函数关系式;
的函数关系式;
(2)根据表中数据写出一个反映日销售量![]() 随时间
随时间![]() 变化的函数关系式;
变化的函数关系式;
(3)在(2)的基础上求该商品的日销售金额的最大值,并求出对应的![]() 值.
值.
(注:日销售金额=每克的销售价格×日销售量)