题目内容
若命题“存在x∈R，2x2-3ax+9＜0”为假命题，则实数a的取值范围是（ ）
A．[-2
| B．[-2，2] | C．[-
| D．（-2
|
“存在x∈R，使2x2-3ax+9＜0”是假命题，
则其否定为真命题，
即是说“?x∈R，都有2x2-3ax+9≥0”，
根据一元二次不等式解的讨论，
可知△=9a2-72≤0，
∴-2
≤a≤2
．
a的取值范围为[-2
，2
]．
故选：A．
则其否定为真命题，
即是说“?x∈R，都有2x2-3ax+9≥0”，
根据一元二次不等式解的讨论，
可知△=9a2-72≤0，
∴-2
| 2 |
| 2 |
a的取值范围为[-2
| 2 |
| 2 |
故选：A．
练习册系列答案
阅读快车系列答案
相关题目
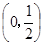
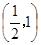
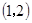
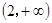
是长方形海域，其中
海里，
海里．现有一架飞机在该海域失事，两艘海事搜救船在
处同时出发，沿直线
、
向前联合搜索，且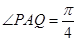
（其中
、
分别在边
、
上），搜索区域为平面四边形
围成的海平面．设
，搜索区域的面积为
．
的关系式，并指出
的值．
：能被3整除的是奇数，
：存在一个能被3整除的整数不是奇数
，
，
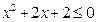时，