题目内容
【题目】2011年,国际数学协会正式宣布,将每年的3月14日设为国际数学节,来源则是中国古代数学家祖冲之的圆周率.祖冲之,在世界数学史上第一次将圆周率(π)值计算到小数点后的第7位,即3.1415926到3.1415927之间,数列{an}是公差大于0的等差数列,其前三项是“31415926”中连续的三个数,数列{bn}是等比数列,其公比大于1的正整数且前三项是“31415926”中的三个数,且a3=b3 .
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)cn= 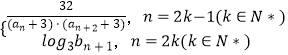 ,求c1+c2+c3+…+c
,求c1+c2+c3+…+c ![]() .(n∈N*)
.(n∈N*)
【答案】解:(Ⅰ)由题可知a1=1,a2=5,a3=9,
b1=4,b2=6,b3=9,
所以an=1+4(n﹣1)=4n﹣3,bn=4× ![]() ;
;
(Ⅱ)由(I)可知cn= 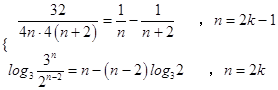 ,
,
则c1+c3+…+ ![]() =1﹣
=1﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() =1﹣
=1﹣ ![]() ,
,
c2+c4+…+ ![]() =(2+4+…+2n)﹣[(2﹣2)+(4﹣2)+(6﹣2)+…+(2n﹣2)]log32
=(2+4+…+2n)﹣[(2﹣2)+(4﹣2)+(6﹣2)+…+(2n﹣2)]log32
= ![]() ﹣[
﹣[ ![]() ﹣2n]log32
﹣2n]log32
=2n﹣1+22n﹣2﹣(22n﹣2﹣2n﹣1)log32,
故所求值为1﹣ ![]() +2n﹣1+22n﹣2﹣(22n﹣2﹣2n﹣1)log32
+2n﹣1+22n﹣2﹣(22n﹣2﹣2n﹣1)log32
【解析】(Ⅰ)通过题干确定数列{an}、{bn}的前三项,进而可得结论;(Ⅱ)通过(I)可求出cn的表达式,利用裂项相消法可知奇数项的和,利用分组求和法可求出偶数项的和,进而相加即得结论.
【考点精析】掌握数列的前n项和是解答本题的根本,需要知道数列{an}的前n项和sn与通项an的关系 .
.

练习册系列答案
相关题目
