题目内容
已知t是正实数,如果不等式组
表示的区域内存在一个半径为1的圆,则t的最小值是( )
|
A、1+
| ||
B、2+2
| ||
| C、1 | ||
| D、2 |
分析:画出满足条件
表示的区域,又由不等式组
表示的区域内存在一个半径为1的圆,我们易分析出x+y=t与圆相切时,t取最小值.
|
|
解答: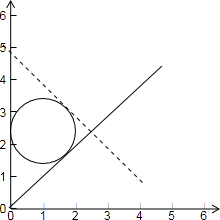 解:不等式组
解:不等式组
表示的区域如下图所示:
由图可知与x-y=0,x=0(Y轴)都相切的半径为1的圆方程为:
(x-1)2+[Y-(1+
)]2=1
若直线x+y=t与圆(x-1)2+[Y-(1+
)]2=1也相切
则t的最小值2+2
故选B
 解:不等式组
解:不等式组
|
由图可知与x-y=0,x=0(Y轴)都相切的半径为1的圆方程为:
(x-1)2+[Y-(1+
| 2 |
若直线x+y=t与圆(x-1)2+[Y-(1+
| 2 |
则t的最小值2+2
| 2 |
故选B
点评:本题考查的知识点是直线与圆的位置关系,其中分析出直线x+y=t与圆相切时,t取最小值,构造出关于t的方程,是解答本题的关键.

练习册系列答案
相关题目
 表示的区域内存在一个半径为1的圆,则t的最小值为 .
表示的区域内存在一个半径为1的圆,则t的最小值为 .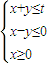 表示的区域内存在一个半径为1的圆,则t的最小值是( )
表示的区域内存在一个半径为1的圆,则t的最小值是( )

 表示的区域内存在一个半径为1的圆,则t的最小值为 。
表示的区域内存在一个半径为1的圆,则t的最小值为 。