题目内容
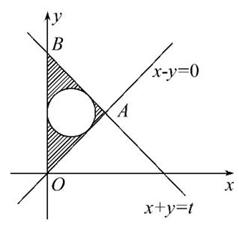
已知t是正实数,如果不等式组
表示的区域内存在一个半径为1的圆,则t的最小值为 .
【解析】画出不等式组表示的平面区域,当t是正实数时,所表示的区域为第一象限的一个等腰直角三角形.依题意,它有一个半径为1的内切圆,不妨设斜边|OB|=t,则两直角边长|AB|=|OA|=
t,所以
=1,求得t=
=2
+2,即tmin=2+2.
答案:2+2
练习册系列答案
相关题目
已知t是正实数，如果不等式组
表示的区域内存在一个半径为1的圆，则t的最小值是（ ）
|
A、1+
| ||
B、2+2
| ||
| C、1 | ||
| D、2 |
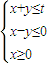表示的区域内存在一个半径为1的圆，则t的最小值是（ ）
表示的区域内存在一个半径为1的圆，则t的最小值为 。