题目内容
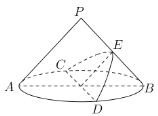
【题目】我们知道：用平行于圆锥母线的平面(不过顶点)截圆锥，则平面与圆锥侧面的交线是抛物线一部分，如图，在底面半径和高均为2的圆锥中，
是底面圆
的两条互相垂直的直径，
是母线
的中点，已知过与的平面与圆锥侧面的交线是以为顶点的圆锥曲线的一部分，则该圆锥曲线的焦点到其准线的距离等于__________.
【答案】
【解析】
如图所示，过点
作
，垂足为
．由于是母线
的中点，圆锥的底面半径和高均为2，可得
．
．在平面
内建立直角坐标系．设抛物线的方程为
，
为抛物线的焦点．可得
，代入解出即可．
解：如图所示，过点作，垂足为．
是母线的中点，圆锥的底面半径和高均为2，
．
．
在平面内建立直角坐标系．
设抛物线的方程为，为抛物线的焦点．
因为，
，解得
．
．即点为
的中点，
该抛物线的焦点到其准线的距离为，
故答案为：．
练习册系列答案
相关题目
