题目内容
椭圆
 的左、右焦点为
的左、右焦点为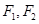 ,过
,过 作直线
作直线 交C于A,B两点,若
交C于A,B两点,若 是等腰直角三角形,且
是等腰直角三角形,且 ,则椭圆C的离心率为( )
,则椭圆C的离心率为( )
A. | B. | C. | D. |
C
解析试题分析:由题意得, ,∴
,∴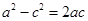 ,∴
,∴ ,∴
,∴ ,
,
∴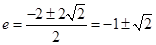 ,∴
,∴ .
.
考点:椭圆的标准方程及性质.

练习册系列答案
相关题目
若 ,则称点
,则称点 在抛物线C:
在抛物线C: 外.已知点
外.已知点 在抛物线C:
在抛物线C: 外,则直线
外,则直线 与抛物线C的位置关系是( )
与抛物线C的位置关系是( )
| A.相交 | B.相切 | C.相离 | D.不能确定 |
已知 为双曲线
为双曲线 的左右焦点,点
的左右焦点,点 在
在 上,
上, ,则
,则 ( )
( )
A. | B. | C. | D. |
方程mx2+y2=1所表示的所有可能的曲线是( )
| A.椭圆、双曲线、圆 |
| B.椭圆、双曲线、抛物线 |
| C.两条直线、椭圆、圆、双曲线 |
| D.两条直线、椭圆、圆、双曲线、抛物线 |
抛物线的顶点在坐标原点,焦点与双曲线 -
- =1的一个焦点重合,则该抛物线的标准方程可能是( )
=1的一个焦点重合,则该抛物线的标准方程可能是( )
| A.x2=4y | B.x2=-4y |
| C.y2=-12x | D.x2=-12y |

 的左、右焦点为
的左、右焦点为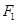 、
、 ,离心率为
,离心率为 ,过
,过 交C于A、B两点,若
交C于A、B两点,若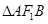 的周长为
的周长为 ,则C的方程为
,则C的方程为 B.
B. C.
C. D.
D.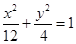
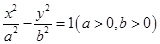 的左、右焦点分别为
的左、右焦点分别为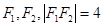 ,P是双曲线右支上的一点,
,P是双曲线右支上的一点,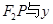 轴交于点A,
轴交于点A,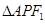 的内切圆在
的内切圆在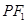 上的切点为Q,若
上的切点为Q,若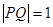 ,则双曲线的离心率是
,则双曲线的离心率是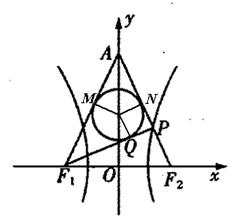
 ,4),则|PA|+|PM|的最小值是( )
,4),则|PA|+|PM|的最小值是( )

 x
x