题目内容
15.已知在△ABC中,a,b,c分别为内角A,B,C的对边,AD是BC边上的中线,G是AD上的点,且$\overrightarrow{AG}$=2$\overrightarrow{GD}$.(1)若(sinA-$\sqrt{3}$sinB)$\overrightarrow{AB}$+(sinC-2sinB)$\overrightarrow{AC}$=$\overrightarrow{0}$,判断△ABC的形状;
(2)若sin2B+sin2C+sinBsinC=sin2A,S△ABC=3,求AG2的最小值.
分析 (1)由题意,sinA-$\sqrt{3}$sinB=0,且sinC-2sinB=0,由正弦定理可得,a=$\sqrt{3}$b,c=2b,结合勾股定理,即可判断△ABC的形状;
(2)先确定A,bc=4$\sqrt{3}$,再利用(2AD)2+a2=2(b2+c2),结合基本不等式确定AD2的最小值是$\sqrt{3}$,利用$\overrightarrow{AG}$=2$\overrightarrow{GD}$.即可求出AG2的最小值.
解答 解:(1)由题意,sinA-$\sqrt{3}$sinB=0,且sinC-2sinB=0,
∴由正弦定理可得,a=$\sqrt{3}$b,c=2b,
∴a2+b2=c2,
∴△ABC是直角三角形;
(2)∵sin2B+sin2C+sinBsinC=sin2A,
由正弦定理可得,a2=b2+c2+bc,
由余弦定理可得,cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=-$\frac{1}{2}$,
∴A=120°
∵S△ABC=3,
∴$\frac{1}{2}$bcsinA=3,
∴bc=4$\sqrt{3}$,
∴(2AD)2+a2=2(b2+c2),
∴4AD2=b2+c2-bc≥bc=4$\sqrt{3}$,
∴AD2的最小值是$\sqrt{3}$,
∵$\overrightarrow{AG}$=2$\overrightarrow{GD}$.
∴AG2的最小值为$\frac{4\sqrt{3}}{9}$.
点评 本题考查正弦定理、余弦定理,考查基本不等式的运用,考查学生分析解决问题的能力,正确运用正弦定理、余弦定理是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.已知三角形的三边长分别为x2+x+1,x2-1和2x+1(x>1),则最大角为( )
| A. | 150° | B. | 120° | C. | 60° | D. | 75° |
5.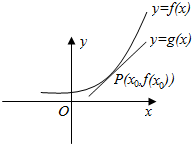 已知可导函数y=f(x)在点P(x0,f(x0))处切线为l:y=g(x)(如图),设F(x)=f(x)-g(x),则( )
已知可导函数y=f(x)在点P(x0,f(x0))处切线为l:y=g(x)(如图),设F(x)=f(x)-g(x),则( )
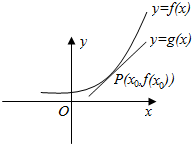 已知可导函数y=f(x)在点P(x0,f(x0))处切线为l:y=g(x)(如图),设F(x)=f(x)-g(x),则( )
已知可导函数y=f(x)在点P(x0,f(x0))处切线为l:y=g(x)(如图),设F(x)=f(x)-g(x),则( )| A. | F′(x0)=0,x=x0是F(x)的极大值点 | B. | F′(x0)=0,x=x0是F(x)的极小值点 | ||
| C. | F′(x0)≠0,x=x0不是F(x)的极值点 | D. | F′(x0)≠0,x=x0是F(x)的极值点 |