题目内容
如图,四边形ABCD为正方形,PA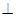 平面ABCD,且AD= 2PA,E、F、G、H分别是线段PA、PD、CD、BC的中点.
平面ABCD,且AD= 2PA,E、F、G、H分别是线段PA、PD、CD、BC的中点.
(I)求证:BC∥平面EFG;
(II)求证:DH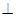 平面AEG.
平面AEG.
(Ⅰ)见解析;(Ⅱ)见解析.
解析试题分析:(Ⅰ)根据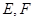 分别为
分别为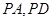 中点,得到
中点,得到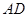 ∥
∥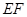 ,
,
根据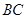 ∥
∥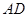 ,推出
,推出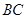 ∥
∥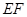 即得证.
即得证.
(Ⅱ)由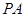 ⊥平面
⊥平面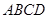 ,得到
,得到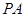 ⊥
⊥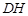 ,即
,即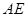 ⊥
⊥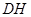 ;
;
再利用△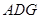 ≌△
≌△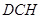 ,可推出∠
,可推出∠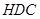 =∠
=∠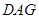 ,∠
,∠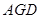 +∠
+∠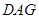 =90°,得到∠
=90°,得到∠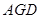 +∠
+∠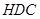 =90°,证得
=90°,证得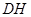 ⊥
⊥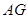 后即得证.
后即得证.
试题解析:(Ⅰ)因为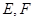 分别为
分别为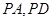 中点,所以
中点,所以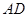 ∥
∥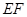 ,
,
因为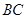 ∥
∥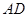 ,所以
,所以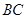 ∥
∥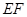 , 2分
, 2分
因为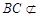 平面
平面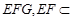 平面
平面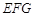 , 4分
, 4分
所以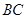 ∥平面
∥平面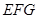 . 6分
. 6分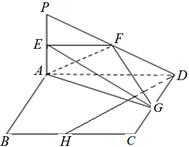
(Ⅱ)因为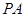 ⊥平面
⊥平面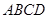 ,所以
,所以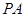 ⊥
⊥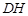 ,
,
即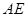 ⊥
⊥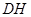 , 8分
, 8分
因为△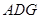 ≌△
≌△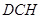 ,
,
所以∠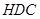 =∠
=∠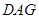 ,
,
∠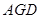 +∠
+∠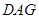 =90°,
=90°,
所以∠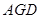 +∠
+∠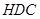 =90°,
=90°,
所以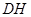 ⊥
⊥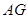 ,
,
又因为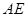 ∩
∩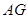 =
= ,所以
,所以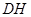 ⊥平面
⊥平面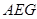 . 12分
. 12分
考点:立体几何的平行关系、垂直关系.

练习册系列答案
相关题目
 中,四边形
中,四边形 为菱形,
为菱形, ,四边形
,四边形 为矩形,若
为矩形,若 ,
, ,
, .
.
 面
面 ;
; 的余弦值;
的余弦值; 中,
中, 平面
平面 ,
, 是正三角形,
是正三角形, 与
与 的交点
的交点 恰好是
恰好是 ,
, ,点
,点 在线段
在线段 上,且
上,且 .
.
 ;
; 平面
平面 ;
; 的余弦值.
的余弦值.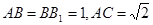 ,直线B1C与平面ABC成45°角。
,直线B1C与平面ABC成45°角。
 中,已知
中,已知 是棱
是棱 的中点.
的中点.
 平面
平面 ,
, ∥平面
∥平面 ;
;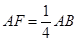
 中,
中,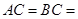
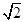 ,且
,且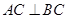 ,点
,点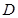 是
是 中点.
中点.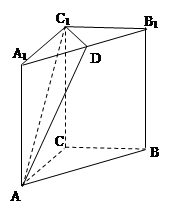
 ⊥平面
⊥平面 ;
;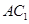 与平面
与平面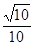 ,
,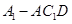 的体积.
的体积.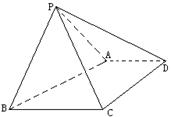
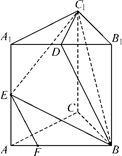
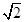 ,AA1=3,D是BC的中点,点E在棱BB1上运动.
,AA1=3,D是BC的中点,点E在棱BB1上运动.