题目内容
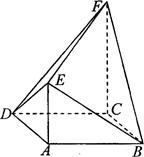
如图,已知在侧棱垂直于底面的三棱柱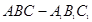 中,
中,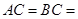
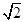 ,且
,且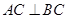 ,点
,点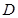 是
是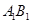 中点.
中点.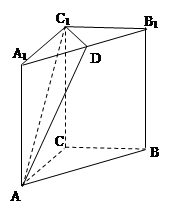
(1)求证:平面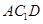 ⊥平面
⊥平面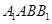 ;
;
(2)若直线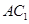 与平面
与平面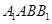 所成角的正弦值为
所成角的正弦值为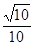 ,
,
求三棱锥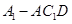 的体积.
的体积.
(1)证明详见解析(2)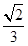
解析试题分析:(1)由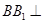 平面
平面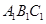 可证
可证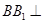
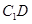 ,由已知条件可得
,由已知条件可得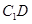
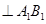 ,,所以在
,,所以在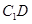
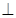 平面
平面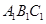 ,然后根据平面与平面垂直的判定定理可得平面
,然后根据平面与平面垂直的判定定理可得平面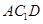 ⊥平面
⊥平面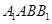 .(2) 先求三角形
.(2) 先求三角形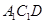 的面积和
的面积和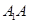 的值,然后再根据棱锥的体积公式求解即可.
的值,然后再根据棱锥的体积公式求解即可.
试题解析:(1)证明: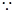
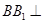 平面
平面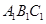 ,
,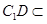 平面
平面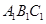 ,
,
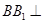
 ,又
,又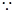
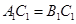 且点
且点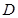 是
是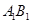 中点.
中点.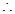
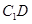
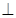 平面
平面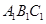 ,又
,又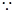
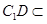 平面
平面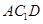 ,
,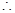 平面
平面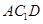 ⊥平面
⊥平面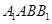 6分
6分
(2)由(1)可知 ,所以AC1与平面A1ABB1所成的角为
,所以AC1与平面A1ABB1所成的角为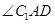 ,在
,在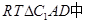 ,由
,由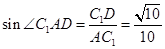 ,
,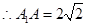

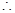
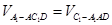 =
=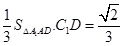 12分
12分
考点:1.直棱柱的性质和平面与平面垂直的判定;2.棱锥的体积.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
正方体 的棱长为
的棱长为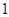 ,线段
,线段 上有两个动点
上有两个动点 ,且
,且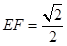 ,则下列结论中错误的是( )
,则下列结论中错误的是( )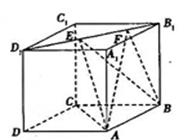
A.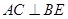 |
B.三棱锥 的体积为定值 的体积为定值 |
C.二面角 的大小为定值 的大小为定值 |
D.异面直线 所成角为定值 所成角为定值 |
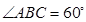 ,
,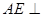 平面ABCD,
平面ABCD,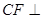 平面ABCD,
平面ABCD,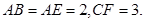
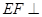 平面BDE;
平面BDE;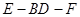 的大小.
的大小. (侧棱和底面垂直的棱柱)中,平面
(侧棱和底面垂直的棱柱)中,平面 侧面
侧面 ,
,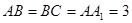 ,
, ,且满足
,且满足 .
.
 ;
;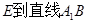 的距离;
的距离; 的平面角的余弦值.
的平面角的余弦值.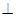 平面ABCD,且AD= 2PA,E、F、G、H分别是线段PA、PD、CD、BC的中点.
平面ABCD,且AD= 2PA,E、F、G、H分别是线段PA、PD、CD、BC的中点.
 为正方形,平面
为正方形,平面 为等腰梯形,
为等腰梯形, ,
,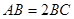 ,
, ,
, .
.
 平面
平面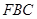 ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值. 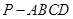 底面是平行四边形,面
底面是平行四边形,面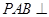 面
面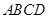 ,
, ,
,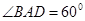 ,
, 分别为
分别为 的中点.
的中点.

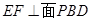
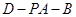 的余弦值.
的余弦值.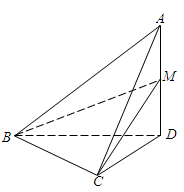
 平面ADC;
平面ADC;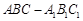 中,
中,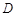 、
、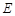 分别是棱
分别是棱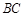 、
、 的中点,点
的中点,点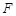 在棱
在棱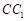 上,已知
上,已知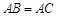 ,
,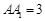 ,
,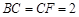 .
.
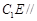 平面
平面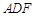 ;
;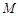 在棱
在棱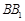 上,当
上,当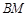 为何值时,平面
为何值时,平面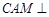 平面
平面