题目内容
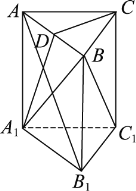
【题目】如图,已知直三棱柱![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ,求证: (1)
,求证: (1)![]() ;
;
(2)![]() ∥平面
∥平面![]() 。
。
【答案】(1)见解析(2)见解析
【解析】
(1)建立空间直角坐标系,设立各点坐标,利用向量数量积证明线线垂直,(2)建立空间直角坐标系,设立各点坐标,利用向量共线证明线线平行,再根据线面平行判定定理得结果.
证明:如图,以C1点为原点,C1A1,C1B1,C1C所在直线分别为x轴、y轴、z轴建立空间直角坐标系.
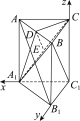
设AC=BC=BB1=2,
则A(2,0,2),B(0,2,2),C(0,0,2),A1(2,0,0),B1(0,2,0),C1(0,0,0),D(1,1,2)。
(1)由于![]() =(0,-2,-2),
=(0,-2,-2),![]() =(-2,2,-2),
=(-2,2,-2),
所以![]()
![]() =0-4+4=0,
=0-4+4=0,
因此![]() ⊥
⊥![]() ,故BC1⊥AB1.
,故BC1⊥AB1.
(2)连接A1C,取A1C的中点E,连接DE,由于E(1,0,1),所以![]() =(0,1,1),又
=(0,1,1),又![]() =(0,-2,-2),
=(0,-2,-2),
所以![]() =-
=-![]() ,又ED和BC1不共线,
,又ED和BC1不共线,
所以ED∥BC1,又DE平面CA1D,
BC1平面CA1D,故BC1∥平面CA1D.

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案【题目】某汽车美容公司为吸引顾客,推出优惠活动:对首次消费的顾客,按200元/次收费,并注册成为会员,对会员逐次消费给予相应优惠,标准如下:
消费次第 | 第1次 | 第2次 | 第3次 | 第4次 | ≥5次 |
收费比例 | 1 |
|
|
|
|
该公司从注册的会员中,随机抽取了![]() 位进行统计,得到统计数据如下:
位进行统计,得到统计数据如下:
消费次第 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
频数 |
|
|
|
|
|
假设汽车美容一次,公司成本为![]() 元.根据所给数据,解答下列问题:
元.根据所给数据,解答下列问题:
(1)估计该公司一位会员至少消费两次的概率;
(2)某会员仅消费两次,求这两次消费中,公司获得的平均利润;
(3)该公司从至少消费两次的顾客中按消费次数用分层抽样方法抽出8人,再从这8人中抽出2人发放纪念品.求抽出的2人中恰有1人消费两次的概率.
【题目】某班主任对全班50名学生学习积极性和参加社团活动情况进行调查,统计数据如表所示
参加社团活动 | 不参加社团活动 | 合计 | |
学习积极性高 | 17 | 8 | 25 |
学习积极性一般 | 5 | 20 | 25 |
合计 | 22 | 28 | 50 |
(Ⅰ)如果随机从该班抽查一名学生,抽到参加社团活动的学生的概率是多少?抽到不参加社团活动且学习积极性一般的学生的概率是多少?
(Ⅱ)试运用独立性检验的思想方法分析:学生的学习积极性与参加社团活动情况是否有关系?并说明理由.
x2=![]() .
.
P(x2≥k) | 0.05 | 0.01 | 0.001 |
K | 3.841 | 6.635 | 10.828 |