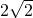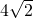题目内容
若Sn为等差数列{an}的前n项和,S9=-36,S13=-104,则a5与a7的等比中项为( )
分析:利用等差数列的求和公式及S9=-36,S13=-104可求首项及公差d,进而可求a5与a7,等比中项为A,则A2=a5•a7,代入可求
解答:解:设等差数列的首项为a1,公差为d
由题意可得,
解可得,a1=4,d=-2
设a5与a7的等比中项为A,则A2=a5•a7=(-4)×(-8)=32
所以,A=±4
故选:C
由题意可得,
|
解可得,a1=4,d=-2
设a5与a7的等比中项为A,则A2=a5•a7=(-4)×(-8)=32
所以,A=±4
| 2 |
故选:C
点评:本题主要考查了等差数列的求和公式的应用,等比中项的应用,属于基础试题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目