题目内容
(三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)(1)(坐标系与参数方程选做题)在直角坐标系中圆C的参数方程为
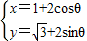 (θ为参数),则圆C的普通方程为 .
(θ为参数),则圆C的普通方程为 .(2)(不等式选讲选做题)设函数f(x)=|2x+1|-|x-4|,则不等式f(x)>2的解集为 .
(3)(几何证明选讲选做题) 如图所示,等腰三角形ABC的底边AC长为6,其外接圆的半径长为5,则三角形ABC的面积是 .

【答案】分析:(1)利用sin2θ+cos2θ=1即可得出;
(2)利用分类讨论的思想方法即可得出;
(3)利用垂径定理及其推论、勾股定理即可得出.
解答:解:(1)圆C的参数方程为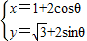 (θ为参数),则圆C的普通方程为
(θ为参数),则圆C的普通方程为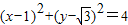 .
.
(2)由函数f(x)=|2x+1|-|x-4|=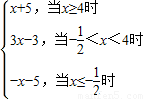 ,
,
解不等式f(x)>2可分为以下三种情况:①由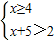 解得x≥4;
解得x≥4;
②由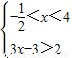 解得
解得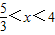 ;
;
③由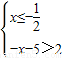 解得x<-7.
解得x<-7.
综上可知:不等式f(x)>2的解集为{x|x<-7或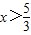 }.
}.
(3)连接OB交AC于E点,∵AB=BC,∴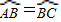 ,∴OB⊥AC,AE=EC=3.
,∴OB⊥AC,AE=EC=3.
在Rt△AOE中,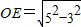 =4,∴BE=1.
=4,∴BE=1.
∴ .
.
故答案为3.
点评:熟练掌握分类讨论的思想方法解绝对值不等式、垂径定理及其推论、勾股定理、平方关系sin2θ+cos2θ=1是解题的关键.
(2)利用分类讨论的思想方法即可得出;
(3)利用垂径定理及其推论、勾股定理即可得出.
解答:解:(1)圆C的参数方程为
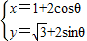 (θ为参数),则圆C的普通方程为
(θ为参数),则圆C的普通方程为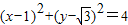 .
.(2)由函数f(x)=|2x+1|-|x-4|=
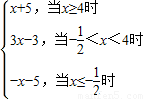 ,
,解不等式f(x)>2可分为以下三种情况:①由
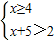 解得x≥4;
解得x≥4;②由
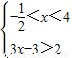 解得
解得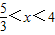 ;
;③由
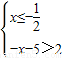 解得x<-7.
解得x<-7.综上可知:不等式f(x)>2的解集为{x|x<-7或
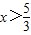 }.
}.(3)连接OB交AC于E点,∵AB=BC,∴
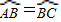 ,∴OB⊥AC,AE=EC=3.
,∴OB⊥AC,AE=EC=3.在Rt△AOE中,
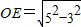 =4,∴BE=1.
=4,∴BE=1.∴
 .
.故答案为3.
点评:熟练掌握分类讨论的思想方法解绝对值不等式、垂径定理及其推论、勾股定理、平方关系sin2θ+cos2θ=1是解题的关键.

练习册系列答案
相关题目
 三选一题(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
三选一题(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (2012•咸阳三模)(考生注意:请在下列三道试题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(2012•咸阳三模)(考生注意:请在下列三道试题中任选一题作答,如果多做,则按所做的第一题评阅记分) (三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (θ为参数),则圆C的普通方程为________.
(θ为参数),则圆C的普通方程为________.