题目内容
 三选一题(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
三选一题(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)A(几何证明选讲)如图,⊙O的两条弦AB,CD相交于圆内一点P,若PA=PB,PC=2,PD=8,OP=4,则该圆的半径长为
B(坐标系与参数方程)曲线C1:
|
|
C(不等式选讲)不等式|2x-1|-|x-2|<0的解集为
分析:A,由相交弦定理,我们结合已知条件可求出PA的值,再由垂径定理,我们根据半弦长、弦心距、圆半径构造直三角形,满足勾股定理,易求出圆的半径;
B,根据已知求出圆的标准方程及直线的一般方程,代入点到直线距离公式,判断直线与圆的位置关系,进而即可求出直线到圆最短离;
C,利用零点分段法,对不等式在x不同的取值范围进行讨论,最后综合讨论结果,即可得到绝对值不等式的解集.
B,根据已知求出圆的标准方程及直线的一般方程,代入点到直线距离公式,判断直线与圆的位置关系,进而即可求出直线到圆最短离;
C,利用零点分段法,对不等式在x不同的取值范围进行讨论,最后综合讨论结果,即可得到绝对值不等式的解集.
解答:解:A、由相交弦定理得:PA•PB=PC•PD,
又∵PA=PB,PC=2,PD=8,
∴PA=4,
由垂径定理得,PO⊥AB
又∵OP=4
∴R=4
故答案为:4
B、曲线C1的标准方程为:(x-1)2+y2=1,表示以(1,0)为圆心,以1为半径的圆,
曲线C2的一般方程为:x+y-1+2
=0
则圆心到直线的距离d=
=2
故直线与圆相离,故直线到圆最短离为2-1=1,
故答案为:1
C、当x>2时,原不等式可化为:x+1<0,此时原不等式不成立;
当
≤x≤2时,原不等式可化为:3x-3<0,解得:
≤x<1;
当x<
时,原不等式可化为:x+1>0,解得:-1<x<
综上原不等式的解集为:(-1,1)
故答案为:(-1,1)
又∵PA=PB,PC=2,PD=8,
∴PA=4,
由垂径定理得,PO⊥AB
又∵OP=4
∴R=4
| 2 |
故答案为:4
| 2 |
B、曲线C1的标准方程为:(x-1)2+y2=1,表示以(1,0)为圆心,以1为半径的圆,
曲线C2的一般方程为:x+y-1+2
| 2 |
则圆心到直线的距离d=
|1-1-2
| ||
|
故直线与圆相离,故直线到圆最短离为2-1=1,
故答案为:1
C、当x>2时,原不等式可化为:x+1<0,此时原不等式不成立;
当
| 1 |
| 2 |
| 1 |
| 2 |
当x<
| 1 |
| 2 |
| 1 |
| 2 |
综上原不等式的解集为:(-1,1)
故答案为:(-1,1)
点评:本题考查的知识点是与圆有关的比例线段,圆的参数方程及绝对值不等式的解法,本题是选修4的选考内容,大家可以根据自己的选修情况,选择一题进行解答.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 (三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (θ为参数),则圆C的普通方程为________.
(θ为参数),则圆C的普通方程为________.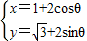 (θ为参数),则圆C的普通方程为 .
(θ为参数),则圆C的普通方程为 .
 上的点到曲线C2:
上的点到曲线C2:
 上的点的最短离为 .
上的点的最短离为 .