题目内容
已知点G是△ABC的重心，O是空间任意一点，若
+
+
=λ
，求λ的值．
| OA |
| OB |
| OC |
| OG |
分析：连结CG并延长，交AB于D，则D为AB中点，且CG=2GD．因此，将
+
+
化成3
+
+
+
，再由三角形重心的性质结合向量的加法法则，算出
+
+
=
，可得
+
+
=3
，得λ=3．
| OA |
| OB |
| OC |
| OG |
| GA |
| GB |
| GC |
| GA |
| GB |
| GC |
| 0 |
| OA |
| OB |
| OC |
| OG |
解答：解 连结CG并延长，交AB于D，则D为AB中点，且CG=2GD，
∴
+
+
=
+
+
+
+
+
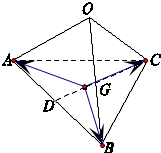=3
+
+
+
∵GD是△GAB的中线，可得
+
=2
∴
+
+
=3
+2
+
∵
=-2
∴
+
+
=3
+2
+（-2
）=3
．
结合
+
+
=λ
，可得λ=3．
∴| OA |
| OB |
| OC |
| OG |
| GA |
| OG |
| GB |
| OG |
| GC |
=3
| OG |
| GA |
| GB |
| GC |
∵GD是△GAB的中线，可得
| GA |
| GB |
| GD |
∴
| OA |
| OB |
| OC |
| OG |
| GD |
| GC |
∵
| GC |
| GD |
∴
| OA |
| OB |
| OC |
| OG |
| GD |
| GD |
| OG |
结合
| OA |
| OB |
| OC |
| OG |
点评：本题给出△ABC的重心G满足向量式
+
+
=λ
，求λ的值．着重考查了平面向量的加法法则、三角形中线的性质和三角形的重心等知识，属于中档题．
| OA |
| OB |
| OC |
| OG |
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
已知点G是△ABC的重心，点P是△GBC内一点，若
=λ
+μ
，则λ+μ的取值范围是（ ）
| AP |
| AB |
| AC |
A、(
| ||
B、(
| ||
C、(1，
| ||
| D、（1，2） |