题目内容
在长方体ABCD-A1B1C1D1中,棱AB=6,BC=BB1=
,点P是线段BC1上的一动点,则AP+PB1的最小值是( )
| 2 |
A、2+
| ||
B、不等的实数根.结合图形可知:k∈(0,
| ||
C、4
| ||
D、5
|
分析:如图,将△BB1C1沿BC1为轴旋转至与平面ABC1共面,得△BB1C1,可得出∠ABB1=135°,由余弦定理求出此时的AB1的长度,再比较四个选项,选出正确答案
解答: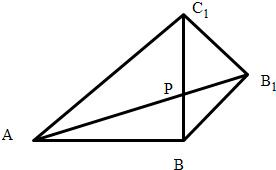 解:如图,将△BB1C1沿BC1为轴旋转至与平面ABC1共面,
解:如图,将△BB1C1沿BC1为轴旋转至与平面ABC1共面,
得△BB1C1,
则∠ABB1=135°,故 AP+PB1=AP+PB1≥AB1=
=5
.
等号当且仅当P为AB2与BC1的交点时取得.
故选D.
 解:如图,将△BB1C1沿BC1为轴旋转至与平面ABC1共面,
解:如图,将△BB1C1沿BC1为轴旋转至与平面ABC1共面,得△BB1C1,
则∠ABB1=135°,故 AP+PB1=AP+PB1≥AB1=
62+(
|
| 2 |
等号当且仅当P为AB2与BC1的交点时取得.
故选D.
点评:本题考查多面体和旋转体表面上的最短距离问题,求解本题的关键是借助图形的翻折,将求折线长度的问题转化为平面上线段长度的问题求解,熟练掌握棱柱的几何特征及余弦定理也求解这个题的知识上的保证.本题易因为没有想起转化方向而导致解题失败

练习册系列答案
相关题目
 在长方体ABCD-A'B'C'D'中,AB=
在长方体ABCD-A'B'C'D'中,AB= 如图,在长方体ABCD-A′B′C′D′中,用截面截下一个棱锥C-A′DD′,求棱锥C-A′DD′的体积与剩余部分的体积之比.
如图,在长方体ABCD-A′B′C′D′中,用截面截下一个棱锥C-A′DD′,求棱锥C-A′DD′的体积与剩余部分的体积之比. (2013•上海) 如图,在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离.
(2013•上海) 如图,在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离. (2009•青浦区二模)(理)在长方体ABCD-A'B'C'D'中,AB=2,AD=1,AA'=1.
(2009•青浦区二模)(理)在长方体ABCD-A'B'C'D'中,AB=2,AD=1,AA'=1. 已知在长方体ABCD-A′B′C′D′中,点E为棱CC′上任意一点,AB=BC=2,CC′=1.
已知在长方体ABCD-A′B′C′D′中,点E为棱CC′上任意一点,AB=BC=2,CC′=1.