题目内容
【题目】设min{m,n}表示m,n二者中较小的一个,已知函数f(x)=x2+8x+14,g(x)=![]() (x>0),若x1∈[-5,a](a≥-4),x2∈(0,+∞),使得f(x1)=g(x2)成立,则a的最大值为
(x>0),若x1∈[-5,a](a≥-4),x2∈(0,+∞),使得f(x1)=g(x2)成立,则a的最大值为
A.-4B.-3C.-2D.0
【答案】C
【解析】
先求得函数![]() 的解析式,并求出它的值域.根据二次函数
的解析式,并求出它的值域.根据二次函数![]() 图像的特点,对
图像的特点,对![]() 分成
分成![]() 和
和![]() 两类讨论,求出使得
两类讨论,求出使得![]() 的值域是
的值域是![]() 值域的子集成立的
值域的子集成立的![]() 的范围,由此求得
的范围,由此求得![]() 的最大值.
的最大值.
令![]() ,解得
,解得![]() ,故当
,故当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,所以
,所以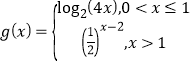 .所以当
.所以当![]() 时,函数
时,函数![]() 的值域为
的值域为![]() ,当
,当![]() 时,
时,![]() 的值域为
的值域为![]() ,所以
,所以![]() 的值域为
的值域为![]() .函数
.函数![]() ,它的图像开口向上,对称轴为
,它的图像开口向上,对称轴为![]() ,则当
,则当![]() 时,函数
时,函数![]() 在
在![]() 上的值域为
上的值域为![]() ,是
,是![]() 的子集,符合题意.当
的子集,符合题意.当![]() 时,函数
时,函数![]() 在
在![]() 上的值域为
上的值域为![]() ,它是
,它是![]() 的子集,故
的子集,故![]() ,解得
,解得![]() .综上所述,满足题意的
.综上所述,满足题意的![]() 的取值范围是
的取值范围是![]() .所以
.所以![]() 的最大值为
的最大值为![]() ,故选C.
,故选C.

练习册系列答案
相关题目
