题目内容
设数列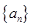 的前
的前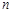 项和
项和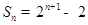 ,数列
,数列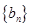 满足
满足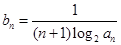 .
.
(1)求数列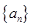 的通项公式;
的通项公式;
(2)求数列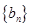 的前
的前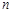 项和
项和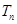 .
.
(1)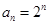 ;(2)
;(2)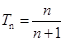 .
.
解析试题分析:本题主要考查由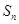 求
求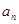 、对数的运算、裂项相消法、等差数列的前n项和公式等基础知识,考查学生的分析问题解决问题的能力、转化能力和计算能力.第一问,由
、对数的运算、裂项相消法、等差数列的前n项和公式等基础知识,考查学生的分析问题解决问题的能力、转化能力和计算能力.第一问,由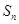 求
求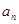 需要分2步:
需要分2步: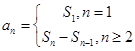 ,在解题的最后需要验证2步是否可以合并成一个式子;第二问,先利用对数式的运算化简
,在解题的最后需要验证2步是否可以合并成一个式子;第二问,先利用对数式的运算化简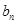 的表达式,根据表达式的特点,利用裂项相消法求数列
的表达式,根据表达式的特点,利用裂项相消法求数列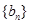 的前n项和.
的前n项和.
试题解析:(1)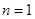 时,
时,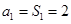 , 2分
, 2分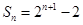 ,∴
,∴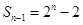
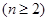
∴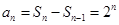
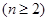 ,
,
∴数列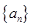 的通项公式为:
的通项公式为: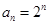 . 6分
. 6分
(2)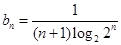
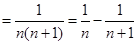 9分
9分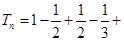
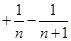
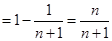 . 12分
. 12分
考点:由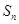 求
求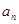 、对数的运算、裂项相消法、等差数列的前n项和公式.
、对数的运算、裂项相消法、等差数列的前n项和公式.

练习册系列答案
相关题目
有一种密英文的明文(真实文)按字母分解,其中英文的a,b,c, ,z的26个字母(不分大小写),依次对应1,2,3, ,26这26个自然数,见如下表格:
| a | b | c | d | e | f | g | h | i | j | k | l | m |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| n | o | p | q | r | s | t | u | v | w | x | y | z |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
给出如下变换公式:
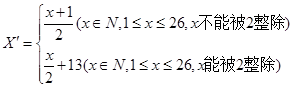
将明文转换成密文,如
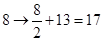 ,即
,即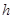 变成
变成 ;如
;如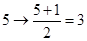 ,即
,即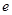 变成
变成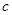 .
.(1)按上述规定,将明文
 译成的密文是什么?
译成的密文是什么?(2)按上述规定,若将某明文译成的密文是
 ,那么原来的明文是什么?
,那么原来的明文是什么? 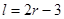 (
(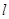 为圆柱的高,
为圆柱的高,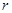 为球的半径,
为球的半径,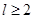 ).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为
).假设该储油罐的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为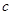 千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为
千元,半球形部分每平方米建造费用为3千元.设该储油罐的建造费用为 千元.
千元.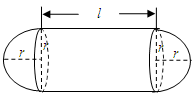
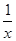 +2的图象关于点A(0,1)对称.
+2的图象关于点A(0,1)对称.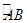 上选择一点C建造垃圾处理厂,其对市区的影响度与所选地
上选择一点C建造垃圾处理厂,其对市区的影响度与所选地 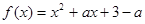 ,
,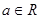 .
. 的取值范围,使
的取值范围,使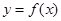 在闭区间
在闭区间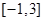 上是单调函数;
上是单调函数;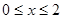 时,函数
时,函数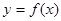 的最大值是关于
的最大值是关于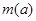 .求
.求
 ,恒有
,恒有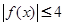 成立.
成立.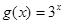 ,
,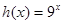 .
.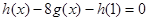 ;
;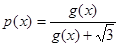 ,求证:
,求证: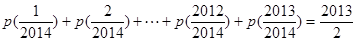 ;
;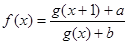 是实数集
是实数集 上的奇函数,且
上的奇函数,且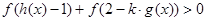 对任意实数
对任意实数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,若在定义域存在实数
,若在定义域存在实数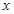 ,满足
,满足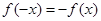 ,则称
,则称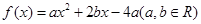 ,试判断
,试判断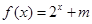 是定义在
是定义在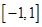 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数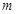 的取值范围.
的取值范围.