题目内容
已知函数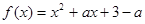 ,
,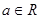 .
.
(1)求 的取值范围,使
的取值范围,使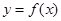 在闭区间
在闭区间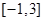 上是单调函数;
上是单调函数;
(2)当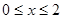 时,函数
时,函数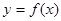 的最大值是关于
的最大值是关于 的函数
的函数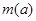 .求
.求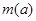 ;
;
(3)求实数 的取值范围,使得对任意的
的取值范围,使得对任意的
 ,恒有
,恒有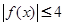 成立.
成立.
(1)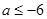 或
或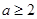 ;(2)
;(2) 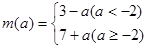 ;(3)
;(3)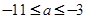 .
.
解析试题分析:(1)求出函数f(x)=x2+ax+3-a图象的对称轴为x=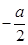 .由f(x)在闭区间[-1,3]上是单调函数,能够求出a的取值范围;(2)当a≥0时,m(a)=f(0)=3-a;当-4≤a<0时,m(a)=f(
.由f(x)在闭区间[-1,3]上是单调函数,能够求出a的取值范围;(2)当a≥0时,m(a)=f(0)=3-a;当-4≤a<0时,m(a)=f(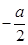 )=
)=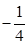 a2-a+3;当a<-4时,m(a)=f(2)=a+7.分段讨论并比较大小得,能够求出m(a)的最大值及;(3)将
a2-a+3;当a<-4时,m(a)=f(2)=a+7.分段讨论并比较大小得,能够求出m(a)的最大值及;(3)将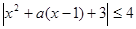 在
在
 时恒成立化成
时恒成立化成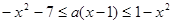 在
在
 时恒成立,分类讨论当
时恒成立,分类讨论当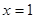 时显然成立,当
时显然成立,当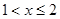 时,
时,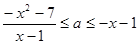 在
在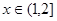 时恒成立,即可求出a的范围.
时恒成立,即可求出a的范围.
解:(1)函数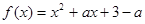 图像的对称轴为
图像的对称轴为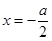 .
.
因为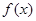 在闭区间
在闭区间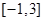 上是单调函数,所以
上是单调函数,所以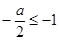 或
或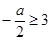 .
.
故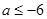 或
或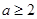 .
.
(2)当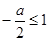 即
即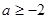 时
时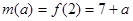
当 即
即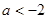 时
时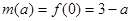
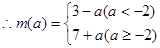
(3)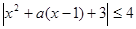 在
在
 时恒成立
时恒成立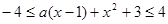 在
在
 时恒成立
时恒成立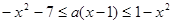 在
在
 时恒成立
时恒成立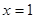 时显然成立
时显然成立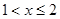 时,
时,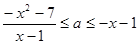 在
在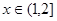 时恒成立
时恒成立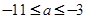 .
.
考点:1.二次函数的性质;2.二次函数在闭区间上的最值.

练习册系列答案
相关题目
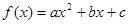 (a≠0)满足
(a≠0)满足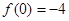 ,
,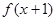 为偶函数,且x=-2是函数
为偶函数,且x=-2是函数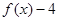 的一个零点.又
的一个零点.又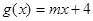 (
( >0).
>0).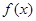 的解析式;
的解析式;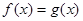 在
在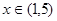 上有解,求实数
上有解,求实数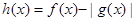 ,求
,求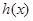 的单调区间.
的单调区间.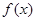 定义在
定义在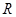 上,对任意的
上,对任意的 ,
,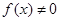 ,且
,且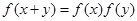 .
.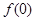 ,并证明:
,并证明: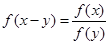 ;
;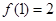 .设向量
.设向量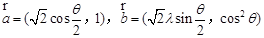 ,对任意
,对任意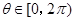 ,
, 恒成立,求实数
恒成立,求实数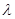 的取值范围.
的取值范围.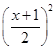 .
.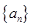 的前
的前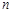 项和
项和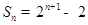 ,数列
,数列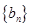 满足
满足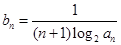 .
.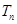 .
.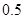 万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变.
万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变.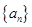 ,每年发放的电动型汽车牌照数为构成数列
,每年发放的电动型汽车牌照数为构成数列 ,完成下列表格,并写出这两个数列的通项公式;
,完成下列表格,并写出这两个数列的通项公式;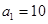
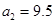
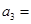
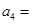
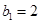

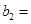 3
3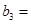
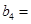
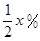 ,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
,该产品每吨的价格上涨百分之几,可使销售的总金额最大? 米,钢筋网的总长度为
米,钢筋网的总长度为 米.
米.
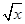 )x万元,假设所有桥墩都视为点且不考虑其他因素,记工程总费用为y万元.
)x万元,假设所有桥墩都视为点且不考虑其他因素,记工程总费用为y万元.