题目内容
湛江为建设国家卫生城市,现计划在相距20 km的赤坎区(记为A)霞山区(记为B)两城区外以AB为直径的半圆弧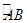 上选择一点C建造垃圾处理厂,其对市区的影响度与所选地
上选择一点C建造垃圾处理厂,其对市区的影响度与所选地
点到市区的距离有关,对赤坎区和霞山区的总影响度为两市区的影响度之和,记C点到赤坎区的距离为x km,建在C处的垃圾处理厂对两市区的总影响度为y.统计调查表明:垃圾处理厂对赤坎区的影响度与所选地点到赤坎区的距离的平方成反比,比例系数为4;对霞山区的影响度与所选地点到霞山区的距离的平方成反比,比例系数为k.当垃圾处理厂建在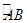 的中点时,对两市区的总影响度为0.065.
的中点时,对两市区的总影响度为0.065.
(1)将y表示成x的函数;
(2)讨论(1)中函数的单调性,并判断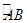 上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到赤坎区的距离;若不存在,说明理由.
上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到赤坎区的距离;若不存在,说明理由.
(1) ;(2)
;(2)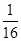 .
.
解析试题分析:(1)根据条件中描述:垃圾处理厂对赤坎区的影响度与所选地点到赤坎区的距离的平方成反比,比例系数为4;对霞山区的影响度与所选地点到霞山区的距离的平方成反比,比例系数为k,而y表示建在C处的垃圾处理厂对两市区的总影响度为y,因此可设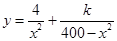 ,根据题意当垃圾处理厂建在
,根据题意当垃圾处理厂建在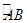 的中点时,对两市区的总影响度为0.065可求得k的值;(2)由(1),
的中点时,对两市区的总影响度为0.065可求得k的值;(2)由(1), ,可求得
,可求得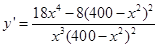 ,进而可以得到y的在(0,20)上的单调性,从而求得y的最小值.
,进而可以得到y的在(0,20)上的单调性,从而求得y的最小值.
(1)如图,由题意知AC⊥BC,AC=x km,则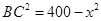 ,
,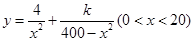 2分
2分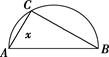
由题意知,当垃圾处理厂建在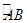 的中点时,对城A和城B的总影响度为0.065,即当
的中点时,对城A和城B的总影响度为0.065,即当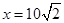 时,y=0.065,代入
时,y=0.065,代入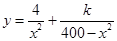 得k=9.所以y表示成x的函数为
得k=9.所以y表示成x的函数为 . 6分;
. 6分;
(2)由于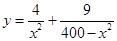 ,∴
,∴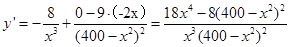 8分
8分
令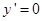 得
得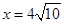 或
或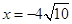 (舍去), 9分
(舍去), 9分
当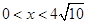 时,
时,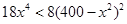 ,即
,即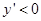 ,此时函数为单调减函数;当
,此时函数为单调减函数;当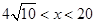 时,
时,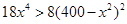 ,即
,即 ,此时函数为单调增函数 12分
,此时函数为单调增函数 12分
所以当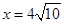 时,即当C点到赤坎区的距离为
时,即当C点到赤坎区的距离为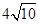 时,函数
时,函数 有最小值
有最小值 14分.
14分.
考点:1、具体情境下函数解析式的求解;2、利用导数判断函数的单调性求最值.

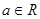 ,函数
,函数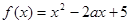 .
.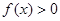 对任意
对任意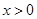 恒成立,求实数
恒成立,求实数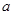 的最值范围;
的最值范围;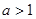 ,且函数
,且函数 的定义域和值域均为
的定义域和值域均为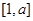 ,求实数
,求实数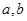 都是实数,且
都是实数,且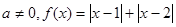 .
. 的解集;
的解集;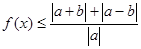 对满足条件的所有实数
对满足条件的所有实数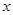 的取值范围.
的取值范围.
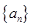 的前
的前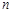 项和
项和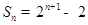 ,数列
,数列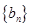 满足
满足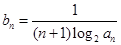 .
.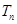 .
.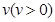 ,雨速沿E移动方向的分速度为
,雨速沿E移动方向的分速度为 。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与
。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与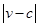 ×S成正比,比例系数为
×S成正比,比例系数为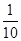 ;(2)其它面的淋雨量之和,其值为
;(2)其它面的淋雨量之和,其值为 ,记
,记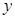 为E移动过程中的总淋雨量,当移动距离d=100,面积S=
为E移动过程中的总淋雨量,当移动距离d=100,面积S=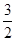 时。
时。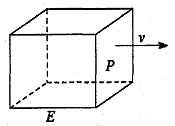
 ,使总淋雨量
,使总淋雨量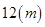 ,高
,高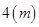 ,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大
,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大 都有|f(x)|≤1成立,试求a的取值范围.
都有|f(x)|≤1成立,试求a的取值范围.