题目内容
设函数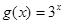 ,
,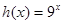 .
.
(1)解方程: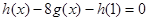 ;
;
(2)令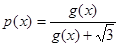 ,求证:
,求证: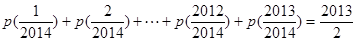 ;
;
(3)若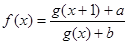 是实数集
是实数集 上的奇函数,且
上的奇函数,且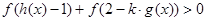 对任意实数
对任意实数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1)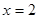 ;(2)参考解析;(3)
;(2)参考解析;(3)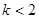
解析试题分析:(1)由于函数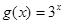 ,
,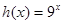 ,所以解方程
,所以解方程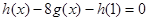 .通过换元即可转化为解二次方程.即可求得结论.
.通过换元即可转化为解二次方程.即可求得结论.
(2)由于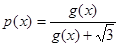 即得到
即得到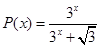 .所以
.所以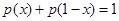 .所以两个一组的和为1,还剩中间一个
.所以两个一组的和为1,还剩中间一个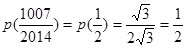 .即可求得结论.
.即可求得结论.
(3)由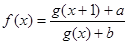 是实数集
是实数集 上的奇函数,可求得
上的奇函数,可求得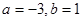 .又由于
.又由于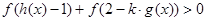 对任意实数
对任意实数 恒成立.该式的理解较困难,所以研究函数
恒成立.该式的理解较困难,所以研究函数 的单调性可得.函数
的单调性可得.函数 在实数集上是递增.集合奇函数,由函数值大小即可得到变量的大小,再利用基本不等式,从而得到结论.
在实数集上是递增.集合奇函数,由函数值大小即可得到变量的大小,再利用基本不等式,从而得到结论.
试题解析:(1)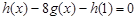 即:
即: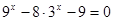 ,解得
,解得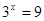 ,
,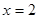
(2)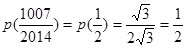 .
.
因为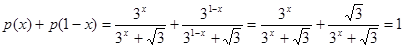 ,
,
所以,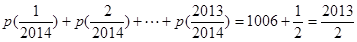 ,
,
(3)因为 是实数集上的奇函数,所以
是实数集上的奇函数,所以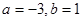 .
.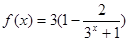 ,
, 在实数集上单调递增.
在实数集上单调递增.
由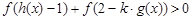 得
得 ,又因为
,又因为 是实数集上的奇函数,所以,
是实数集上的奇函数,所以,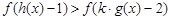 ,
,
又因为 在实数集上单调递增,所以
在实数集上单调递增,所以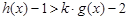
即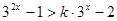 对任意的
对任意的 都成立,
都成立,
即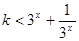 对任意的
对任意的 都成立,
都成立,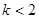 .
.
考点:1.解方程的思想.2.函数的单调性.3.归纳推理的思想.4.基本不等式.

练习册系列答案
相关题目
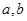 都是实数,且
都是实数,且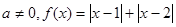 .
. 的解集;
的解集;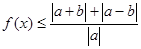 对满足条件的所有实数
对满足条件的所有实数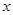 的取值范围.
的取值范围.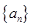 的前
的前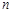 项和
项和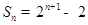 ,数列
,数列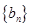 满足
满足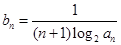 .
.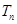 .
.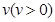 ,雨速沿E移动方向的分速度为
,雨速沿E移动方向的分速度为 。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与
。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与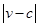 ×S成正比,比例系数为
×S成正比,比例系数为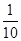 ;(2)其它面的淋雨量之和,其值为
;(2)其它面的淋雨量之和,其值为 ,记
,记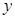 为E移动过程中的总淋雨量,当移动距离d=100,面积S=
为E移动过程中的总淋雨量,当移动距离d=100,面积S=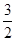 时。
时。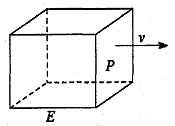
 ,使总淋雨量
,使总淋雨量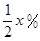 ,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
,该产品每吨的价格上涨百分之几,可使销售的总金额最大?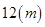 ,高
,高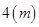 ,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大
,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大 ,若在定义域内存在实数
,若在定义域内存在实数 ,满足
,满足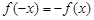 ,则称
,则称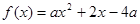
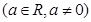 ,试判断
,试判断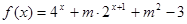 为定义域
为定义域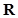 上的“局部奇函数”,求实数m的取值范围.
上的“局部奇函数”,求实数m的取值范围.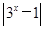 的图象,并利用图象回答:k为何值时,方程
的图象,并利用图象回答:k为何值时,方程