题目内容
设数列{an}的前n项和为Sn,令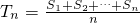 ,称Tn为数列a1,a2,…,an的“和平均数”,已知数列a1,a2,…,a502的“和平均数”为2012,那么数列2,a1,a2,…,a502的“和平均数”为________.
,称Tn为数列a1,a2,…,an的“和平均数”,已知数列a1,a2,…,a502的“和平均数”为2012,那么数列2,a1,a2,…,a502的“和平均数”为________.
2010
分析:根据定义有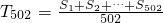 =2012,整理得,S1+S2+…S502=2012×502①.再利用定义数列2,a1,a2,…,a502的“和平均数”为T503=
=2012,整理得,S1+S2+…S502=2012×502①.再利用定义数列2,a1,a2,…,a502的“和平均数”为T503=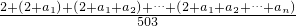 转化为
转化为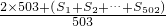 代入①求解.
代入①求解.
解答:数列a1,a2,…,a502的“和平均数”为2012,根据定义即有:
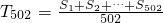 =2012,
=2012,
整理得,S1+S2+…S502=2012×502.
数列2,a1,a2,…,a502的“和平均数”为
T503=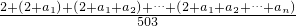
=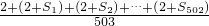
=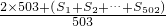
=2+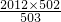
=2+2008=2010
故答案为:2010.
点评:本题考查数列的有关运算,是新定义题型.本题根据定义得出相应的已知表达式,和未知的所求式,并建立两式的联系,进行求解.
分析:根据定义有
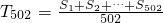 =2012,整理得,S1+S2+…S502=2012×502①.再利用定义数列2,a1,a2,…,a502的“和平均数”为T503=
=2012,整理得,S1+S2+…S502=2012×502①.再利用定义数列2,a1,a2,…,a502的“和平均数”为T503=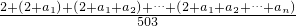 转化为
转化为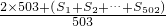 代入①求解.
代入①求解.解答:数列a1,a2,…,a502的“和平均数”为2012,根据定义即有:
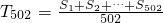 =2012,
=2012,整理得,S1+S2+…S502=2012×502.
数列2,a1,a2,…,a502的“和平均数”为
T503=
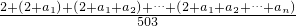
=
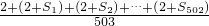
=
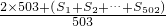
=2+
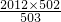
=2+2008=2010
故答案为:2010.
点评:本题考查数列的有关运算,是新定义题型.本题根据定义得出相应的已知表达式,和未知的所求式,并建立两式的联系,进行求解.

练习册系列答案
相关题目