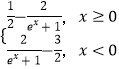题目内容
【题目】是否存在a，b，c使等式（ 
）2+（ 
）2+（ 
）2+…+（ 
）2= 
对一切n∈N*都成立若不存在，说明理由；若存在，用数学归纳法证明你的结论．
【答案】解：取n=1，2，3可得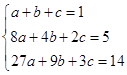 
解得：a= 
，b= 
，c= 
． 下面用数学归纳法证明（ 
）2+（ 
）2+（ 
）2+…+（ 
）2= 
= 
．
即证12+22+…+n2= n（n+1）（2n+1），
①n=1时，左边=1，右边=1，∴等式成立；
②假设n=k时等式成立，即12+22+…+k2= k（k+1）（2k+1）成立，
则当n=k+1时，等式左边=12+22+…+k2+（k+1）2═ k（k+1）（2k+1）+（k+1）2= [k（k+1）（2k+1）+6（k+1）2]= （k+1）（2k2+7k+6）= （k+1）（k+2）（2k+3），
∴当n=k+1时等式成立；
由数学归纳法，综合①②当n∈N*等式成立，
故存在a= ，b= ，c= 使已知等式成立
【解析】分别取n=1，2，3，得到关于a，b，c的方程组解得即可，先根据当n=1时，把n=1代入求值等式成立；再假设n=k时关系成立，利用变形可得n=k+1时关系也成立，综合得到对于任意n∈N*时都成立
【考点精析】认真审题，首先需要了解数学归纳法的定义(数学归纳法是证明关于正整数n的命题的一种方法)．
练习册系列答案
相关题目
【题目】下表是某厂的产量x与成本y的一组数据：
产量x（千件） | 2 | 3 | 5 | 6 |
成本y（万元） | 7 | 8 | 9 | 12 |
（Ⅰ）根据表中数据，求出回归直线的方程 
= 
x 
（其中 = 
， 
= 
﹣ 
）
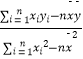（Ⅱ）预计产量为8千件时的成本．
