题目内容
已知幂函数 的图象与x轴,y轴无交点且关于原点对称,又有函数f(x)=x2-alnx+m-2在(1,2]上是增函数,g(x)=x-
的图象与x轴,y轴无交点且关于原点对称,又有函数f(x)=x2-alnx+m-2在(1,2]上是增函数,g(x)=x- 在(0,1)上为减函数.
在(0,1)上为减函数.
①求a的值;
②若 ,数列{an}满足a1=1,an+1=p(an),(n∈N+),数列{bn},满足
,数列{an}满足a1=1,an+1=p(an),(n∈N+),数列{bn},满足 ,
, ,求数列{an}的通项公式an和sn.
,求数列{an}的通项公式an和sn.
③设 ,试比较[h(x)]n+2与h(xn)+2n的大小(n∈N+),并说明理由.
,试比较[h(x)]n+2与h(xn)+2n的大小(n∈N+),并说明理由.
① ;②
;② ;
; ;③见解析.
;③见解析.
解析试题分析:①由幂函数的定义和性质可以知道 的取值集合,由图像关于原点对称的函数是奇函数可以确定
的取值集合,由图像关于原点对称的函数是奇函数可以确定 的值,将
的值,将 的值代入
的值代入 ,
, 的解析式后,根据函数的单调性与导函数的关系以及不等式的恒成立问题的解法就可以知道
的解析式后,根据函数的单调性与导函数的关系以及不等式的恒成立问题的解法就可以知道 满足的不等式,就可以解得
满足的不等式,就可以解得 的值;②先由已知条件求出
的值;②先由已知条件求出 的解析式,然后得出
的解析式,然后得出 ,
, 的关系,由函数构造的方法可以求得
的关系,由函数构造的方法可以求得 的解析式,代入
的解析式,代入 即可,再由数列求和公式求得
即可,再由数列求和公式求得 的值;③先求出
的值;③先求出 的解析式,再由相减的方法来判断两个式子的大小,最后减得的结果和0比较即可,注意分类讨论的思想.
的解析式,再由相减的方法来判断两个式子的大小,最后减得的结果和0比较即可,注意分类讨论的思想.
试题解析:①幂函数的图像与 轴,
轴, 轴无交点,则有
轴无交点,则有 ,解得
,解得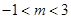
又 ,∴
,∴ 或
或 ,
,
又幂函数的图像关于原点对称,则有幂函数是奇函数,
当 时,
时, 是偶函数,不合题意,舍去,
是偶函数,不合题意,舍去,
当 时,
时, 是奇函数,∴
是奇函数,∴ ,
,
∴ ,求导得
,求导得 ,
,
又∵ 在
在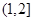 上是增函数,∴
上是增函数,∴ 在
在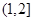 上恒成立,
上恒成立,
解得 ,
,
又∵ ,
, 在
在 上为减函数,
上为减函数,
∴ 在
在 上恒成立,
上恒成立,
解得 ,
,
综上知 ; ..3分
; ..3分
②∵ ,
,
∴ ∴
∴ ∴
∴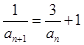 ∴
∴ ,
,
∴ 是首项为
是首项为 公比
公比 的等比数列,
的等比数列,
∴ 解得
解得 ,
,
∴ ,
,
∴ ,
, ; .6分
; .6分
③∵ ,
,
当 时,
时, ,
,
当 时,
时,
=
=
=
=
 ,
, . 10分
. 10分
考点:函数的单调性与导函数的关系,奇函数图像的性质,等比数列的构造.

练习册系列答案
相关题目
 来拟合该景点对外开放的第
来拟合该景点对外开放的第
 年与当年的游客人数
年与当年的游客人数 (单位:万人)之间的关系.
(单位:万人)之间的关系. =
= ,试确定
,试确定 的值,并考察该函数是否符合上述两点预测;
的值,并考察该函数是否符合上述两点预测; ,欲使得该函数符合上述两点预测,试确定
,欲使得该函数符合上述两点预测,试确定 的取值范围.
的取值范围. 的定义域为
的定义域为 .
. 的取值范围;
的取值范围; 的不等式
的不等式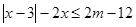 .
. .
. ,解不等式
,解不等式 ;
; ,
, ,求实数
,求实数 的取值范围.
的取值范围. (
( )在区间
)在区间 上有最大值
上有最大值 和最小值
和最小值 .设
.设 .
. 、
、 的值;
的值; 在
在 上有解,求实数
上有解,求实数 的取值范围.
的取值范围. ,
, 
 .
. , 函数
, 函数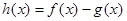 在其定义域是增函数,求
在其定义域是增函数,求 的取值范围;
的取值范围;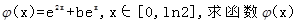 的最小值;
的最小值; 的图象
的图象 与函数
与函数 的图象
的图象 交于点
交于点 ,过线段
,过线段 的中点
的中点 作
作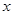 轴的垂线分别交
轴的垂线分别交 、
、 ,问是否存在点
,问是否存在点 ,若在定义域内存在实数
,若在定义域内存在实数 ,满足
,满足 ,则称
,则称 ,试判断
,试判断 是定义在区间
是定义在区间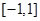 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围;
的取值范围; 为定义域
为定义域 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 .
. 时,
时, 取得极值,求
取得极值,求 的值;
的值; ,当
,当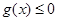 在其定义域内恒成立,并证明
在其定义域内恒成立,并证明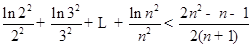 (
( ).
). 的定义域为
的定义域为 ,若
,若 在
在 上为增函数,则称
上为增函数,则称 为“一阶比增函数”.
为“一阶比增函数”. 是“一阶比增函数”,求实数
是“一阶比增函数”,求实数 的取值范围;
的取值范围; ,
, ;
; 有解.
有解.