题目内容
已知四棱锥P-ABCD,底面ABCD为矩形,侧棱PA⊥底面ABCD,其中BC=2AB=2PA=6,M,N为侧棱PC上的两个三等分点,如图所示.(1)求证:AN∥平面MBD;
(2)求异面直线AN与PD所成角的余弦值;
(3)求二面角M-BD-C的余弦值.
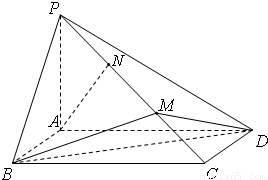
【答案】分析:(1)连接AC交BD于O,连接OM,可得OM∥AN,再利用直线与平面平行的判定定理进行证明,即可解决问题;
(2)如图所示,以A为原点,建立空间直角坐标系A-xyz,写出各点的坐标,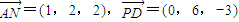 ,AN与PD的夹角就是异面直线AN与PD所成角,然后求出其余弦值.
,AN与PD的夹角就是异面直线AN与PD所成角,然后求出其余弦值.
(3)侧棱PA⊥底面ABCD,可得平面BCD的一个法向量为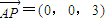 ,设平面MBD的法向量为m=(x,y,z),两个法向量的夹角就是二面角M-BD-C,然后再求出其余弦值.
,设平面MBD的法向量为m=(x,y,z),两个法向量的夹角就是二面角M-BD-C,然后再求出其余弦值.
解答: (Ⅰ)证明:连接AC交BD于O,连接OM,
(Ⅰ)证明:连接AC交BD于O,连接OM,
∵底面ABCD为矩形,
∴O为AC中点,(1分)
∵M、N为侧棱PC的三等分点,
∴CM=MN,
∴OM∥AN,(3分)
∵OM?平面MBD,AN不属于平面MBCD,
∴AN∥平面MBD.(4分)
(Ⅱ)如图所示,以A为原点,建立空间直角坐标系A-xyz,
则A(0,0,0),B(3,0,0),C(3,6,0),D(0,6,0),P(0,0,3),M(2,4,1),N(1,2,2),
∵ ,(5分)
,(5分)
∴ ,(7分)
,(7分)
∴异面直线AN与PD所成角的余弦值为 .(8分)
.(8分)
(Ⅲ)∵侧棱PA⊥底面ABCD,
∴平面BCD的一个法向量为 ,(9分)
,(9分)
设平面MBD的法向量为m=(x,y,z),
∵ ,并且
,并且 ,
,
∴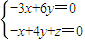 ,
,
令y=1得x=2,z=-2,
∴平面MBD的一个法向量为m=(2,1,-2).(11分)
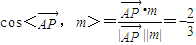 (13分)
(13分)
由图可知二面角M-BD-C的大小是锐角,
∴二面角M-BD-C大小的余弦值为 .(14分)
.(14分)
点评:此题考查直线与平面平行的判断及平面与平面的夹角问题,此题建立直角坐标系比较简单,万一找不到面面角,用向量法求解也是可以的,这种做题思想要记住,此类立体几何题是每年高考必考的一道大题,同学们要课下要多练习.
(2)如图所示,以A为原点,建立空间直角坐标系A-xyz,写出各点的坐标,
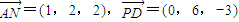 ,AN与PD的夹角就是异面直线AN与PD所成角,然后求出其余弦值.
,AN与PD的夹角就是异面直线AN与PD所成角,然后求出其余弦值.(3)侧棱PA⊥底面ABCD,可得平面BCD的一个法向量为
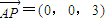 ,设平面MBD的法向量为m=(x,y,z),两个法向量的夹角就是二面角M-BD-C,然后再求出其余弦值.
,设平面MBD的法向量为m=(x,y,z),两个法向量的夹角就是二面角M-BD-C,然后再求出其余弦值.解答:
 (Ⅰ)证明:连接AC交BD于O,连接OM,
(Ⅰ)证明:连接AC交BD于O,连接OM,∵底面ABCD为矩形,
∴O为AC中点,(1分)
∵M、N为侧棱PC的三等分点,
∴CM=MN,
∴OM∥AN,(3分)
∵OM?平面MBD,AN不属于平面MBCD,
∴AN∥平面MBD.(4分)
(Ⅱ)如图所示,以A为原点,建立空间直角坐标系A-xyz,
则A(0,0,0),B(3,0,0),C(3,6,0),D(0,6,0),P(0,0,3),M(2,4,1),N(1,2,2),
∵
 ,(5分)
,(5分)∴
 ,(7分)
,(7分)∴异面直线AN与PD所成角的余弦值为
 .(8分)
.(8分)(Ⅲ)∵侧棱PA⊥底面ABCD,
∴平面BCD的一个法向量为
 ,(9分)
,(9分)设平面MBD的法向量为m=(x,y,z),
∵
 ,并且
,并且 ,
,
∴
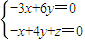 ,
,令y=1得x=2,z=-2,
∴平面MBD的一个法向量为m=(2,1,-2).(11分)
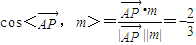 (13分)
(13分)由图可知二面角M-BD-C的大小是锐角,
∴二面角M-BD-C大小的余弦值为
 .(14分)
.(14分)点评:此题考查直线与平面平行的判断及平面与平面的夹角问题,此题建立直角坐标系比较简单,万一找不到面面角,用向量法求解也是可以的,这种做题思想要记住,此类立体几何题是每年高考必考的一道大题,同学们要课下要多练习.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点.
如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点. 如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC,侧面PBC⊥底面ABCD,O是BC的中点.
如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC,侧面PBC⊥底面ABCD,O是BC的中点. 已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,E为BC中点,AE与BD交于O点,AB=BC=2CD=2,BD⊥PE.
已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,E为BC中点,AE与BD交于O点,AB=BC=2CD=2,BD⊥PE. 如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠DAB=∠ABC=90°,E是线段PC上一点,PC⊥平面BDE.
如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠DAB=∠ABC=90°,E是线段PC上一点,PC⊥平面BDE.