题目内容
3. 如图,在四棱锥P-ABCD中,底面ABCD是梯形,PA⊥底面ABCD,其中BA⊥AD,AD∥BC,AC与BD交于点O,M是AB边上的点,且$BM=\frac{1}{3}BA$,已知PA=AD=4,AB=3,BC=2.
如图,在四棱锥P-ABCD中,底面ABCD是梯形,PA⊥底面ABCD,其中BA⊥AD,AD∥BC,AC与BD交于点O,M是AB边上的点,且$BM=\frac{1}{3}BA$,已知PA=AD=4,AB=3,BC=2.(Ⅰ)求平面PAD与平面PMC所成锐二面角的正切值;
(Ⅱ)已知N是PM上一点,且ON∥平面PCD,求$\frac{PM}{PN}$的值.
分析 (1)连接CM并延长交DA的延长线于E,说明∠MFA是平面PMC与平面PAD所成锐二面角的平面角然后求解tan∠MFA=$\frac{MA}{FA}$,得到结果.
(2)连接MO并延长交CD于G,连接PG,在△BAD中,通过$\frac{BO}{OD}=\frac{BM}{MA}$,说明MO∥AD,然后求解$\frac{PM}{PN}$的值.
解答 解:(1)连接CM并延长交DA的延长线于E,则PE是平面PMC与平面PAD所成二面角的棱,
过A作AF垂直PE于F,连接MF.
∵PA⊥平面ABCD,∴PA⊥MA,
又MA⊥AD,∴MA⊥平面PAD,
∵AF⊥PE,∴MF⊥PE,
∴∠MFA是平面PMC与平面PAD所成锐二面角的平面角…(3分)
∵BC=2,AD=4,BC∥AD,AM=2MB,
∴AE=4,又PA=4,∴AF=2$\sqrt{2}$,
∴tan∠MFA=$\frac{MA}{FA}=\frac{\sqrt{2}}{2}$,
所以平面PMC与平面PAD所成锐二面角的正切为$\frac{\sqrt{2}}{2}$.…(6分)
(2)连接MO并延长交CD于G,连接PG,
∵ON∥平面PCD,∴ON∥PG,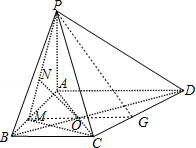
在△BAD中∵$\frac{BO}{OD}=\frac{BC}{AD}=\frac{1}{2}$,又$\frac{BM}{MA}=\frac{1}{2}$,
∴$\frac{BO}{OD}=\frac{BM}{MA}$,
∴MO∥AD,…(9分)
又在直角梯形ABCD中,由$\frac{MO}{BC}=\frac{AM}{AB}$,$\frac{OG}{AD}=\frac{OC}{AC}$,可得:MO=OG=$\frac{4}{3}$,
∵ON∥PG,
∴PN=MN,
∴$\frac{PM}{PN}=2$.…(12分)
点评 本题考查二面角的平面角的求法,几何法与向量法的应用,考查空间想象能力以及计算能力,考查了推理论证能力,属于中档题.

| A. | {-5,$\frac{1}{2}$} | B. | {-5,$\frac{1}{2}$,2} | C. | {-5,2} | D. | {2,$\frac{1}{2}$} |
 如图所示,已知⊙O1与⊙O2相交于A、B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1、⊙O2于点D、E,DE与AC相交于点P.
如图所示,已知⊙O1与⊙O2相交于A、B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1、⊙O2于点D、E,DE与AC相交于点P.