题目内容
(本小题满分8分)设函数 的图象在
的图象在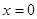 处的切线方程为
处的切线方程为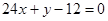 .
.
(Ⅰ)求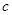 ,
, ;
;
(Ⅱ)若函数在 处取得极值
处取得极值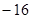 ,试求函数解析式并确定函数的单调区间.
,试求函数解析式并确定函数的单调区间.
 的图象在
的图象在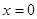 处的切线方程为
处的切线方程为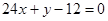 .
.(Ⅰ)求
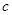 ,
, ;
;(Ⅱ)若函数在
 处取得极值
处取得极值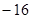 ,试求函数解析式并确定函数的单调区间.
,试求函数解析式并确定函数的单调区间.解:(Ⅰ)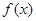 的定义域为
的定义域为 ,
,
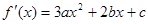 ,∴
,∴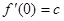 ; -----------------1分
; -----------------1分
∵切线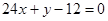 的斜率为
的斜率为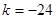 ,∴
,∴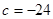 ; -----------------2分
; -----------------2分
把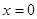 代入
代入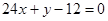 得
得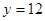 ,∴P(0,12), -----------------3分
,∴P(0,12), -----------------3分
∴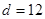 .
.
∴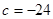 ,
,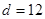 . -----------------4分
. -----------------4分
(Ⅱ)由(Ⅰ)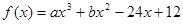
由已知得: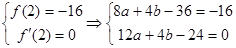
∴ -----------------5分
-----------------5分
∴
∴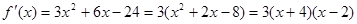 -----------------6分
-----------------6分
由 得,
得,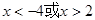 ;
;
由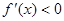 得,
得,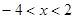 ; -----------------7分
; -----------------7分
∴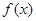 的单调增区间为
的单调增区间为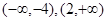 ;
;
单调减区间为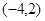 . -----------------8分
. -----------------8分
 的定义域为
的定义域为 ,
,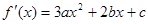 ,∴
,∴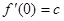 ; -----------------1分
; -----------------1分∵切线
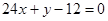 的斜率为
的斜率为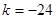 ,∴
,∴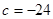 ; -----------------2分
; -----------------2分把
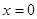 代入
代入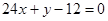 得
得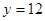 ,∴P(0,12), -----------------3分
,∴P(0,12), -----------------3分∴
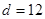 .
.∴
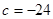 ,
,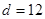 . -----------------4分
. -----------------4分(Ⅱ)由(Ⅰ)
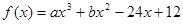
由已知得:
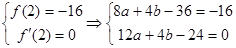
∴
 -----------------5分
-----------------5分∴

∴
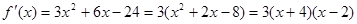 -----------------6分
-----------------6分由
 得,
得,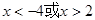 ;
;由
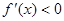 得,
得,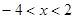 ; -----------------7分
; -----------------7分∴
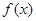 的单调增区间为
的单调增区间为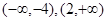 ;
;单调减区间为
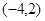 . -----------------8分
. -----------------8分略

练习册系列答案
相关题目
 为定义在
为定义在 上的可导函数,且
上的可导函数,且 对于
对于 恒成立且e为自然对数的底,则
恒成立且e为自然对数的底,则 与
与 的大小关系是
的大小关系是 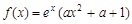
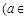 R).
R).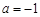 ,求曲线
,求曲线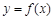 在点
在点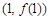 处的的切线方程;
处的的切线方程; 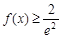 对任意
对任意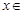
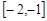 恒成立,求实数
恒成立,求实数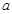 的取值范围.
的取值范围.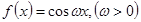 将
将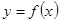 的图象向右平移
的图象向右平移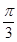 个单位长
个单位长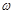 的最小值等于( )
的最小值等于( )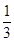
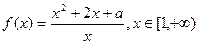
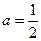 时,求函数
时,求函数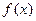 的最小值;
的最小值;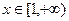 ,
,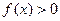 恒成立,试求实数
恒成立,试求实数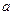 的取值范围.
的取值范围.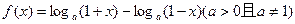
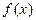 的奇偶性与单调性;
的奇偶性与单调性;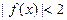 的解集为
的解集为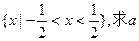 的值;
的值;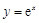 的图象在点
的图象在点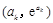 处的切线与
处的切线与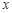 轴的交点的横坐标为
轴的交点的横坐标为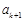 ,其中
,其中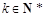 ,
,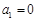 ,则
,则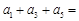
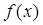 是偶函数,当
是偶函数,当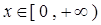 时,
时,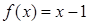 ,则
,则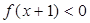 解集为:
解集为: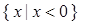



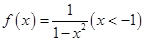 ,则
,则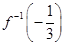 的值是( )
的值是( )