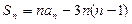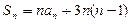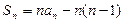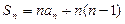题目内容
已知数集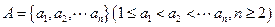 具有性质
具有性质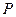 ;对任意的
;对任意的
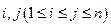 ,
,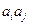 与
与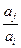 两数中至少有一个属于
两数中至少有一个属于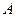 。
。
(Ⅰ)分别判断数集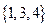 与
与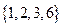 是否具有性质
是否具有性质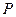 ,并说明理由;
,并说明理由;
(Ⅱ)证明: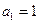 ,且
,且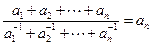 ;
;
(Ⅲ)证明:当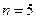 时,
时,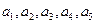 成等比数列。
成等比数列。
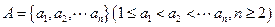 具有性质
具有性质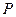 ;对任意的
;对任意的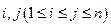 ,
,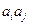 与
与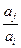 两数中至少有一个属于
两数中至少有一个属于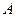 。
。(Ⅰ)分别判断数集
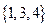 与
与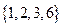 是否具有性质
是否具有性质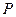 ,并说明理由;
,并说明理由;(Ⅱ)证明:
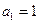 ,且
,且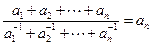 ;
;(Ⅲ)证明:当
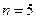 时,
时,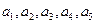 成等比数列。
成等比数列。(Ⅰ)由于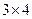 与
与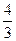 均不属于数集
均不属于数集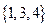 ,∴该数集不具有性质P;由于
,∴该数集不具有性质P;由于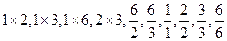 都属于数集
都属于数集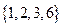 ,∴该数集具有性质P。
,∴该数集具有性质P。
(Ⅱ)证明见解析。
(Ⅲ)证明见解析。
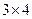 与
与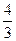 均不属于数集
均不属于数集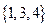 ,∴该数集不具有性质P;由于
,∴该数集不具有性质P;由于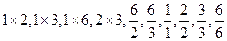 都属于数集
都属于数集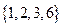 ,∴该数集具有性质P。
,∴该数集具有性质P。(Ⅱ)证明见解析。
(Ⅲ)证明见解析。
本题主要考查集合、等比数列的性质,考查运算能力、推理论证能力、分
分类讨论等数学思想方法。本题是数列与不等式的综合题,属于较难层次题。
(Ⅰ)由于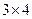 与
与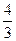 均不属于数集
均不属于数集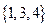 ,∴该数集不具有性质P;由于
,∴该数集不具有性质P;由于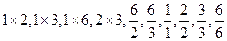 都属于数集
都属于数集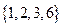 ,∴该数集具有性质P。
,∴该数集具有性质P。
(Ⅱ)∵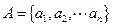 具有性质P,∴
具有性质P,∴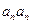 与
与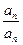 中至少有一个属于A,
中至少有一个属于A,
由于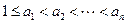 ,∴
,∴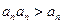 ,故
,故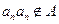 。
。
从而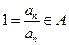 ,∴
,∴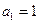 。
。
∵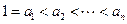 , ∴
, ∴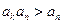 ,故
,故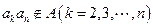 。
。
由A具有性质P可知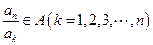 。
。
又∵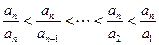 ,
,
∴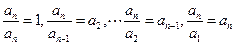 ,
,
从而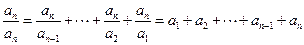 ,
,
∴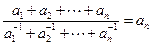 。
。
(Ⅲ)由(Ⅱ)知,当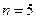 时,有
时,有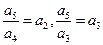 ,即
,即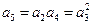 ,
,
∵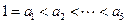 ,∴
,∴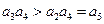 ,∴
,∴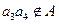 ,
,
由A具有性质P可知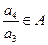 。
。
由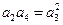 ,得
,得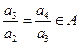 ,且
,且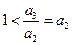 ,∴
,∴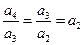 ,
,
∴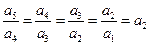 ,即
,即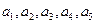 是首项为1,公比为
是首项为1,公比为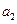 成等比数列。
成等比数列。
分类讨论等数学思想方法。本题是数列与不等式的综合题,属于较难层次题。
(Ⅰ)由于
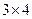 与
与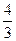 均不属于数集
均不属于数集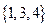 ,∴该数集不具有性质P;由于
,∴该数集不具有性质P;由于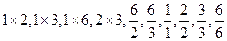 都属于数集
都属于数集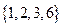 ,∴该数集具有性质P。
,∴该数集具有性质P。(Ⅱ)∵
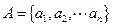 具有性质P,∴
具有性质P,∴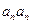 与
与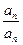 中至少有一个属于A,
中至少有一个属于A,由于
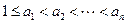 ,∴
,∴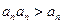 ,故
,故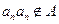 。
。从而
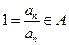 ,∴
,∴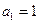 。
。∵
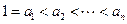 , ∴
, ∴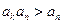 ,故
,故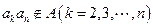 。
。由A具有性质P可知
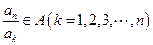 。
。又∵
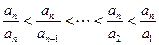 ,
,∴
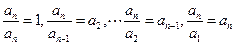 ,
,从而
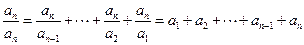 ,
,∴
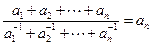 。
。(Ⅲ)由(Ⅱ)知,当
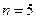 时,有
时,有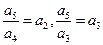 ,即
,即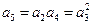 ,
,∵
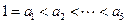 ,∴
,∴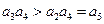 ,∴
,∴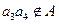 ,
,由A具有性质P可知
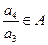 。
。由
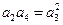 ,得
,得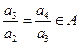 ,且
,且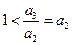 ,∴
,∴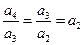 ,
,∴
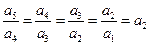 ,即
,即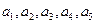 是首项为1,公比为
是首项为1,公比为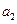 成等比数列。
成等比数列。
练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
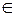
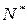 ),其中
),其中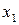 为正实数.
为正实数. 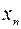 表示xn+1;
表示xn+1;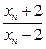 ,证明数列{
,证明数列{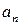 }成等比数列,并求数列{xn}的通项公式;
}成等比数列,并求数列{xn}的通项公式;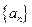 的前n项和
的前n项和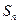 ,
,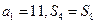 .
.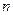 ;(2)求
;(2)求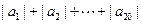 的值.
的值.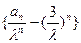 是等差数列,公差为2,
是等差数列,公差为2,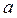 1,=11,
1,=11,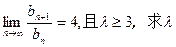 的值; (Ⅱ)在(Ⅰ)条件下,求数列{
的值; (Ⅱ)在(Ⅰ)条件下,求数列{ }的前n项和.
}的前n项和.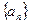 的首项
的首项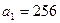 ,前n项和为
,前n项和为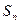 ,且
,且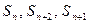 成等差数列.
成等差数列.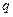 ;
;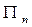 表示
表示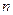 项之积,即
项之积,即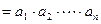 ,试比较
,试比较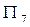 、
、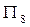 、
、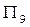 的大小.
的大小.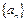 中,
中,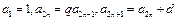 (
(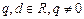 ).
).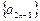 是等比数列,且
是等比数列,且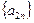 是等差数列,求q, d满足的条件.
是等差数列,求q, d满足的条件.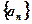 中,
中,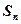 是其前
是其前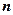 项和,
项和,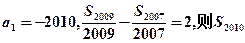 的值为
的值为  的值;
的值; ,是否存在一个实数
,是否存在一个实数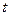 ,使数列
,使数列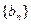 为等差数列?若存在,求出实数
为等差数列?若存在,求出实数 }的前n项和
}的前n项和
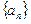 的公差为2,前
的公差为2,前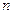 项和为
项和为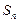 ,则下列结论中正确的是 ( )
,则下列结论中正确的是 ( )