题目内容
11.不等式|2-3x|>4的解集用区间表示为(-$∞,-\frac{2}{3}$)∪(2,+∞).分析 运用|x|>a?-a>x或x>a,求解不等式,解出即可.
解答 解:不等式|2-3x|>4即为:3x-2>4,或3x-2<-4
即为:x>2或x<-$\frac{2}{3}$,
则解集为:(-$∞,-\frac{2}{3}$)∪(2,+∞),
故答案为:(-$∞,-\frac{2}{3}$)∪(2,+∞).
点评 本题考查绝对值不等式的解法,考查运算能力,属于基础题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
6.已知集合A到B的映射f:(xy)→(x+y,xy),那么集合A中元素(4,3)在B中所对应的元素是( )
| A. | (1,3) | B. | (3,1) | C. | (7,12) | D. | (12,7) |
5.已知命题p:1<2x<8;命题q:不等式x2-mx+4≥0恒成立,若?p是?q的必要条件,实数m的取值范围为( )
| A. | (0,4) | B. | (-∞,4] | C. | [4,+∞) | D. | (0,4] |
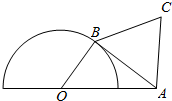 如图所示,半圆O的直径为2,A为半圆直径的延长线上的一点,且OA=2,B为半圆上任一点,以AB为边向右上方作等边△ABC.
如图所示,半圆O的直径为2,A为半圆直径的延长线上的一点,且OA=2,B为半圆上任一点,以AB为边向右上方作等边△ABC.