题目内容
【题目】已知函数![]() ,有下列四个结论:
,有下列四个结论:
①![]() 为偶函数;②
为偶函数;②![]() 的值域为
的值域为![]() ;
;
③![]() 在
在![]() 上单调递减;④
上单调递减;④![]() 在
在![]() 上恰有8个零点,
上恰有8个零点,
其中所有正确结论的序号为( )
A.①③B.②④C.①②③D.①③④
【答案】A
【解析】
由偶函数的定义可判断①正确,借助二倍角公式将函数化简为 利用二次函数性质计算可得②错误,利用复合函数的单调性可判断
利用二次函数性质计算可得②错误,利用复合函数的单调性可判断![]() 在
在![]() 上单调递减,且
上单调递减,且![]() ,则
,则![]() 在
在![]() 上单调递增,根据偶函数性质可得出③正确,利用函数与方程的思想解方程即可判断④错误.
上单调递增,根据偶函数性质可得出③正确,利用函数与方程的思想解方程即可判断④错误.
由![]() ,故
,故![]() 为偶函数,①正确;
为偶函数,①正确;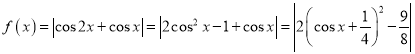 ,
,
记![]() ,则
,则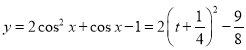 ,
,
当![]() 时,
时,![]() 取得最大值2,当
取得最大值2,当![]() 时,
时,![]() 取9得最小值
取9得最小值![]() ,
,
即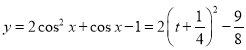 的值域为
的值域为![]() ,所以
,所以![]() 的值域为
的值域为![]() ,②错误;
,②错误;
![]() 在
在![]() 上的单调性与它在
上的单调性与它在![]() 上的单调性刚好相反,
上的单调性刚好相反,
当![]() 时,
时,![]() 单调递增,且
单调递增,且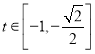 ,而
,而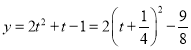 在
在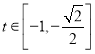 时单调递减,
时单调递减,
故![]() 在
在![]() 上单调递减,又此时
上单调递减,又此时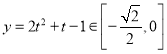 ,故函数
,故函数![]() 在
在![]() 上单调递增,于是得
上单调递增,于是得![]() 在
在![]() 单调递减,③正确;
单调递减,③正确;
令![]() ,得
,得![]() 或
或![]() ,而当
,而当![]() 时,
时,![]() 及
及![]() 恰有3个不等的实根
恰有3个不等的实根![]() ,
,![]() ,
,![]() ,
,
即![]() 在区间
在区间![]() 上恰有3个零点,结合奇偶性可知,即
上恰有3个零点,结合奇偶性可知,即![]() 在区间
在区间![]() 上恰有6个零点,④错误.
上恰有6个零点,④错误.
故正确的是①③.
故选:A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】今年情况特殊,小王在居家自我隔离时对周边的水产养殖产业进行了研究.![]() 、
、![]() 两个投资项目的利润率分别为投资变量
两个投资项目的利润率分别为投资变量![]() 和
和![]() .根据市场分析,
.根据市场分析,![]() 和
和![]() 的分布列分别为:
的分布列分别为:
| 5% | 10% | ||
| 0.8 | 0.2 | ||
| 2% | 8% | 12% | |
| 0.2 | 0.5 | 0.3 | |
(1)若在![]() 两个项目上各投资
两个项目上各投资![]() 万元,
万元,![]() 和
和![]() 分别表示投资项目
分别表示投资项目![]() 和
和![]() 所获得的利润,求方差
所获得的利润,求方差![]() ,
,![]() ;
;
(2)若在![]() 两个项目上共投资
两个项目上共投资![]() 万元,那么如何分配,能使投资
万元,那么如何分配,能使投资![]() 项目所得利润的方差与投资
项目所得利润的方差与投资![]() 项目所得利润的方差的和最小,最小值是多少?
项目所得利润的方差的和最小,最小值是多少?
(注:![]() )
)