题目内容
判断下列函数在给定区间上是否存在零点.
(1)f(x)=x3+1;
(2)f(x)= -x,x∈(0,1).
-x,x∈(0,1).
 解:(1)∵f(x)=x3+1=(x+1)(x2-x+1),
解:(1)∵f(x)=x3+1=(x+1)(x2-x+1),令f(x)=0,即(x+1)(x2-x+1)=0,∴x=-1,
∴f(x)=x3+1有零点-1.
(2)法一:令f(x)=0得
 -x=0,
-x=0,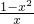 =0,
=0,∴x=±1,而±1∉(0,1),
∴f(x)=
 -x,x∈(0,1)不存在零点.
-x,x∈(0,1)不存在零点.法二:令y1=
 ,y2=x,在同一平面直角坐标系中,作出它们的图象,从图中可以看出当0<x<1时,两图象没有交点.
,y2=x,在同一平面直角坐标系中,作出它们的图象,从图中可以看出当0<x<1时,两图象没有交点.故f(x)=
 -x,x∈(0,1)没有零点.
-x,x∈(0,1)没有零点.分析:(1)令f(x)=x3+1=0,解方程得x=-1,由此可得函数在给定区间上存在零点;
(2)方法一:令
 -x=0解得x的值不在定义域内,故函数不存在零点;
-x=0解得x的值不在定义域内,故函数不存在零点;方法二:令y1=
 ,y2=x,在同一平面直角坐标系中,作出它们的图象,从图中可以看出当0<x<1时,两图象没有交点.
,y2=x,在同一平面直角坐标系中,作出它们的图象,从图中可以看出当0<x<1时,两图象没有交点.故相应的函数没有零点.
点评:本题考查函数的零点的性问题,借用了零点与方程根的关系转化为求方程的根,有根则函数有零点,方法二用作图法确定函数是否有零点.

练习册系列答案
相关题目
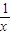 -x,x∈(0,1).
-x,x∈(0,1).