题目内容
判断下列函数在给定区间上是否存在零点.
(1)f(x)=x2-3x-18,x∈[1,8];
(2)f(x)=x3-x-1,x∈[-1,2];
(3)f(x)=log2(x+2)-x,x∈[1,3].
答案:
解析:
提示:
解析:
|
(1)解法1:∵f(1)=-20<0,f(8)=22>0, ∴f(1)·f(8)<0.故f(x)=x2-3x-18在[1,8]上存在零点. 解法2:∴令x2-3x-18=0,解得x=-3或x=6, ∴函数f(x)=x2-3x-18在[1,8]上存在零点. (2)∵f(-1)=-1<0,f(2)=5>0, ∴f(-1)·f(2)<0,∴f(x)=x3-x-1在[1,2]上存在零点. (3)∵f(1)=log2(1+2)-1>log22-1=0, f(3)=log2(3+2)-3<log28-3=0. ∴f(1)·f(3)<0,故f(x)=log2(x+2)-x在[1,3]上存在零点. |
提示:
|
分析:利用函数零点的存在性或图象进行判断. 评注:(1)题利用零点的存在性定理或直接求出函数零点,(2)(3)利用零点的存在性定理求解. |

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 -x,x∈(0,1).
-x,x∈(0,1).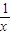 -x,x∈(0,1).
-x,x∈(0,1).