题目内容
判断下列函数在给定区间上是否存在零点.
(1)f(x)=x2-3x-18,x∈[1,8];
(2)f(x)=x3-x-1,x∈[-1,2];
(3)f(x)=log2(x+2)-x,x∈[1,3].
(1)存在零点(2)存在零点(3) 存在零点
解析:
(1)方法一 因为f(1)=-20<0,f(8)=22>0,
所以f(1)·f(8)<0,故f(x)=x2-3x-18,x∈[1,8]存在零点.
方法二 令x2-3x-18=0,解得x=-3或6,
所以函数f(x)=x2-3x-18,x∈[1,8]存在零点.
(2)∵f(-1)=-1<0,f(2)=5>0,
∴f(x)=x3-x-1,x∈[-1,2]存在零点.
(3)∵f(1)=log2(1+2)-1>log22-1=0.
f(3)=log2(3+2)-3<log28-3=0.∴f(1)·f(3)<0
故f(x)=log2(x+2)-x在x∈[1,3]上存在零点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 -x,x∈(0,1).
-x,x∈(0,1).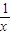 -x,x∈(0,1).
-x,x∈(0,1).