题目内容
15.已知f(x)=|2x-4|,g(x)=|x+3|.(1)解不等式f(x)+g(x)>7;
(2)令h(x)=f(x)+2g(x),求h(x)的最小值,并求出当h(x)取的最小值时x的取值范围.
分析 (1)把要求得不等式去掉绝对值,化为与之等价的3个不等式组,求得每个不等式组的解集,再取并集,即得所求.
(2)利用绝对值三角不等式求得h(x)的最小值,可得此时x的取值范围.
解答 解:(1)不等式f(x)+g(x)>7,即|2x-4|+|x+3|>7,、
等价于 $\left\{\begin{array}{l}{x<-3}\\{4-2x-x-3>7}\end{array}\right.$①,或$\left\{\begin{array}{l}{-3≤x≤2}\\{4-2x+x+3>7}\end{array}\right.$②,或$\left\{\begin{array}{l}{x>2}\\{2x+4+x+3>7}\end{array}\right.$③.
解①求得 x<-3,解②求得-3≤x<0,解③求得x>$\frac{8}{3}$,
综上可得,不等式的解集为(∞,0)∪($\frac{8}{3}$,+∞).
(2)h(x)=f(x)+2g(x)=|2x-4|+|2x+6|≥|2x-4-(2x+6)|=10,
故h(x)的最小值为10.此时,-3≤x≤2,
故当h(x)取的最小值时x的取值范围为[-3,2].
点评 本题主要考查绝对值不等式的解法,绝对值三角不等式,体现了转化、分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
4.如果x∈(0,π),则y=cosx+2sinx的值域是( )
| A. | [-$\sqrt{5}$,$\sqrt{5}$] | B. | (-1,1) | C. | (-1,$\sqrt{5}$] | D. | (-1,2] |
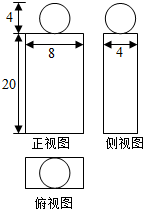 己知一几何体的三视图,试根据三视图计算出它的表面积和体积(结果保留π).
己知一几何体的三视图,试根据三视图计算出它的表面积和体积(结果保留π).