题目内容
【题目】抛物线
的焦点为
，斜率为正的直线
过点交抛物线于
、
两点，满足
.
（1）求直线的斜率；
（2）过焦点与垂直的直线交抛物线于
、
两点，求四边形
的面积.
【答案】（1）
（2）81
【解析】
（1）设直线
的方程，联立直线与抛物线方程，化简后由韦达定理表示出
，
，根据
可由向量的坐标关系求得参数，得直线方程的斜率.
（2）根据题意，表示出直线
的方程，联立抛物线可得
，由（1）可求得
，即可由对角线互相垂的性质直求得四边形
的面积.
（1）依题意知
，设直线的方程为
，
；
将直线的方程与抛物线的方程联立
；
消去
得
.设
，
；
所以
，
； ①
因为，得
； ②
联立①和②，消去
，
，得
，
又，则
；
故直线的斜率是
；
（2）由条件有
，
∴直线的斜率
；
则直线的方程
；
将直线的方程与抛物线的方程联立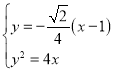
；
化简可得
；
设
，
，
∴
；
∴
；
由（1）知
；
∴
；
；
所以
，
四边形的面积为81.
练习册系列答案
相关题目
