题目内容
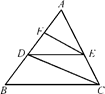
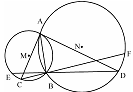
如图,圆 与圆
与圆 交于
交于 两点,以
两点,以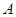 为切点作两圆的切线分别交圆
为切点作两圆的切线分别交圆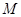 和圆
和圆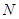 于
于 两点,延长
两点,延长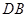 交圆
交圆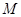 于点
于点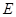 ,延长
,延长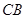 交圆
交圆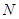 于点
于点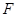 .已知
.已知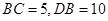 .
.
(1)求 的长;
的长;
(2)求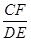 .
.
(1)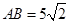 ;(2)
;(2)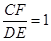 .
.
解析试题分析:本题主要考查弦切角定理、三角形相似、切割线定理等基础知识,考查学生的逻辑推理能力、分析问题解决问题的能力.第一问,由于AC、AD分别是圆N、圆M的切线,所以利用弦切角定理,得到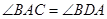 ,
,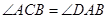 ,所以相似三角形的判定,得△
,所以相似三角形的判定,得△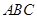 ∽△
∽△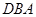 ,所以可得到边的比例关系,从而求出边长;第二问,根据切割线定理,得到2组关系式,2个式子相除得到一个等式,再结合第一问的结论,解方程,得到
,所以可得到边的比例关系,从而求出边长;第二问,根据切割线定理,得到2组关系式,2个式子相除得到一个等式,再结合第一问的结论,解方程,得到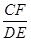 的值.
的值.
试题解析:(1)根据弦切角定理,知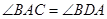 ,
,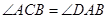 ,
,
∴△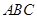 ∽△
∽△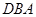 ,则
,则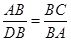 ,
,
故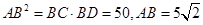 . 5分
. 5分
(2)根据切割线定理,知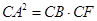 ,
,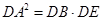 ,
,
两式相除,得 (*)
(*)
由△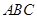 ∽△
∽△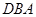 ,得
,得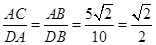 ,
,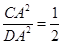 ,
,
又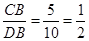 ,由(*)得
,由(*)得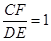 . 10分
. 10分
考点:弦切角定理、三角形相似、切割线定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
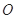 的直径
的直径 ,
,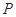 是
是 延长线上一点,
延长线上一点, ,割线
,割线 交圆
交圆 ,
,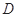 ,过点
,过点 的垂线,交直线
的垂线,交直线 于点
于点 ,交直线
,交直线 于点
于点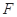 .
. ;
; 的值.
的值.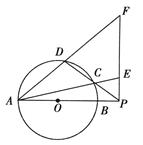
 中,
中, 是的∠A的平分线,圆
是的∠A的平分线,圆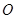 经过点
经过点 与
与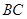 切于点
切于点 ,与
,与 相交于
相交于 ,连结
,连结 ,
, .
. ; (2)求证:
; (2)求证: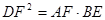 .
.



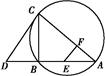

 ,求AF的长.
,求AF的长.