题目内容
已知命题p:“a=1是x>0,x+
≥2的充分必要条件”,命题q:“存在x0∈R,x02+x0-2>0”,则下列命题正确的是( )
| a |
| x |
| A.命题“p∧q”是真命题 | B.命题“p∧(¬q)”是真命题 |
| C.命题“(¬p)∧q”是真命题 | D.命题“(¬p)∧(¬q)”是真命题 |
对于p,当a=1时,x+
≥2
=2,在x>0时恒成立,
反之,若x>0,x+
≥2恒成立,则2
≥2,即
≥1,可得a≥1
因此,“a=1是x>0,x+
≥2的充分不必要条件”,命题p是假命题.
对于q,∵在x0<-1或x0>2时x02+x0-2>0才成立,
∴“存在x0∈R,x02+x0-2>0”是真命题,即命题q是真命题.
综上,命题p为假命题而命题q为真命题,所以命题“(¬p)∧q”是真命题
故选C
| 1 |
| x |
x•
|
反之,若x>0,x+
| a |
| x |
x•
|
| a |
因此,“a=1是x>0,x+
| a |
| x |
对于q,∵在x0<-1或x0>2时x02+x0-2>0才成立,
∴“存在x0∈R,x02+x0-2>0”是真命题,即命题q是真命题.
综上,命题p为假命题而命题q为真命题,所以命题“(¬p)∧q”是真命题
故选C

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
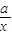 ≥2的充分必要条件”,命题q:“存在x∈R,
≥2的充分必要条件”,命题q:“存在x∈R,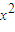 +x-2>0”,则下列命题正确的是( )
+x-2>0”,则下列命题正确的是( )