题目内容
已知命题p:a=1;命题q:复数z=(a2-1)+(a-2)i(a,b∈R)为纯虚数.则p是q的( )
分析:当a=1时,复数z的是不为0,虚部为-1,当复数z为纯虚数时,需要其实部为0,虚部不等于0.结合充要条件的判断方法即可得出答案.
解答:解:当a=1时,z=-i为纯虚数;
反之,若z是纯虚数,则
,解得:a=±1,
所以“a=1”是“z为纯虚数”的充分不必要条件.
故选A.
反之,若z是纯虚数,则
|
所以“a=1”是“z为纯虚数”的充分不必要条件.
故选A.
点评:本题考查了必要条件、充分条件与充要条件的判断,判断充要条件的方法是:
①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件;
②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件;
③若p⇒q为真命题且q⇒p为真命题,则命题p是命题q的充要条件;
④若p⇒q为假命题且q⇒p为假命题,则命题p是命题q的即不充分也不必要条件.
⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.
①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件;
②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件;
③若p⇒q为真命题且q⇒p为真命题,则命题p是命题q的充要条件;
④若p⇒q为假命题且q⇒p为假命题,则命题p是命题q的即不充分也不必要条件.
⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
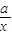 ≥2的充分必要条件”,命题q:“存在x∈R,
≥2的充分必要条件”,命题q:“存在x∈R,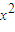 +x-2>0”,则下列命题正确的是( )
+x-2>0”,则下列命题正确的是( )