题目内容
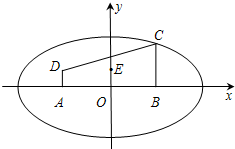 如图,在直角坐标系xOy中有一直角梯形ABCD,AB的中点为O,AD⊥AB,AD∥BC,AB=4,BC=3,AD=1,以A,B为焦点的椭圆经过点C.
如图,在直角坐标系xOy中有一直角梯形ABCD,AB的中点为O,AD⊥AB,AD∥BC,AB=4,BC=3,AD=1,以A,B为焦点的椭圆经过点C.(1)求椭圆的标准方程;
(2)若点E(0,1),问是否存在直线l与椭圆交于M,N两点且|ME|=|NE|,若存在,求出直线l的斜率的取值范围;若不存在,请说明理由.
分析:(1)根据题意,确定CA+CB=8,从而可确定椭圆的几何量,即可求椭圆的标准方程;
(2)将直线l:y=kx+m与椭圆联立,利用|ME|=|NE|,取MN中点F,利用kEF•k=-1及判别式,即可得出直线l的斜率的取值范围.
(2)将直线l:y=kx+m与椭圆联立,利用|ME|=|NE|,取MN中点F,利用kEF•k=-1及判别式,即可得出直线l的斜率的取值范围.
解答: 解:(1)∵AB=4,BC=3,AD⊥AB,AD∥BC
解:(1)∵AB=4,BC=3,AD⊥AB,AD∥BC
∴AC=5
∴CA+CB=8>AB=4
∴a=4
∵c=2,∴b2=12
∴椭圆的标准方程为
+
=1
(2)设直线l:y=kx+m,M(x1,y1),N(x2,y2)
将直线l:y=kx+m与椭圆联立可得
,消去y得
∴
①
,
设MN中点F(x0,y0),
,
∵|ME|=|NE|,∴EF⊥MN,∴kEF•k=-1,∴
•k=-1,
∴m=-(4k2+3)
代入①可得:16k2+12>(4k2+3)2
∴16k4+8k2-3<0
∴-
<k<
∴k∈(-
,
)
 解:(1)∵AB=4,BC=3,AD⊥AB,AD∥BC
解:(1)∵AB=4,BC=3,AD⊥AB,AD∥BC∴AC=5
∴CA+CB=8>AB=4
∴a=4
∵c=2,∴b2=12
∴椭圆的标准方程为
| x2 |
| 16 |
| y2 |
| 12 |
(2)设直线l:y=kx+m,M(x1,y1),N(x2,y2)
将直线l:y=kx+m与椭圆联立可得
|
|
∴
|
|
|
|
设MN中点F(x0,y0),
|
|
∵|ME|=|NE|,∴EF⊥MN,∴kEF•k=-1,∴
| ||
|
∴m=-(4k2+3)
代入①可得:16k2+12>(4k2+3)2
∴16k4+8k2-3<0
∴-
| 1 |
| 2 |
| 1 |
| 2 |
∴k∈(-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查存在性问题的探究,解题的关键是直线与椭圆方程联立,利用韦达定理进行求解.

练习册系列答案
相关题目
 (2009•杭州二模)如图,在直角坐标系xOy中,锐角△ABC内接于圆x2+y2=1.已知BC平行于x轴,AB所在直线方程为y=kx+m(k>0),记角A,B,C所对的边分别是a,b,c.
(2009•杭州二模)如图,在直角坐标系xOy中,锐角△ABC内接于圆x2+y2=1.已知BC平行于x轴,AB所在直线方程为y=kx+m(k>0),记角A,B,C所对的边分别是a,b,c. 如图,在直角坐标系中,中心在原点,焦点在X轴上的椭圆G的离心率为
如图,在直角坐标系中,中心在原点,焦点在X轴上的椭圆G的离心率为 (2013•石景山区二模)如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且
(2013•石景山区二模)如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且 如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且
如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且 如图,在直角坐标系中,已知射线OA:x-y=0(x≥0),OB:
如图,在直角坐标系中,已知射线OA:x-y=0(x≥0),OB: