题目内容
1955年，印度数学家卡普耶卡（D.R.Kaprekar）研究了对四位自然数的一种交换：任给出四位数
，用的四个数字由大到小重新排列成一个四位数m，再减去它的反序数n(即将的四个数字由小到大排列，规定反序后若左边数字有0，则将0去掉运算，比如0001，计算时按1计算)，得出数
，然后继续对
重复上述变换，得数
，…，如此进行下去，卡普耶卡发现，无论是多大的四位数，只要四个数字不全相同，最多进行k次上述变换，就会出现变换前后相同的四位数t(这个数称为Kaprekar变换的核).通过研究10进制四位数2014可得Kaprekar变换的核为 .
，用的四个数字由大到小重新排列成一个四位数m，再减去它的反序数n(即将的四个数字由小到大排列，规定反序后若左边数字有0，则将0去掉运算，比如0001，计算时按1计算)，得出数，然后继续对重复上述变换，得数，…，如此进行下去，卡普耶卡发现，无论是多大的四位数，只要四个数字不全相同，最多进行k次上述变换，就会出现变换前后相同的四位数t(这个数称为Kaprekar变换的核).通过研究10进制四位数2014可得Kaprekar变换的核为 .6174
试题分析：把5 298代入计算，用5 298的四个数字由大到小重新排列成一个四位数9852．则9852-2589=7263，用7263的四个数字由大到小重新排列成一个四位数7632．则7632-2367=5265，用5265的四个数字由大到小重新排列成一个四位数6552．则6552-2556=3996，用3996的四个数字由大到小重新排列成一个四位数9963．则9963-3699=6264，用6264的四个数字由大到小重新排列成一个四位数6642．则6642-2466=4176，用4176的四个数字由大到小重新排列成一个四位数7641．则7641-1467=6174，用6174的四个数字由大到小重新排列成一个四位数7641．则7641-1467=6174…可知7次变换之后，四位数最后都会停在一个确定的数6174上．同样地，把4 852代入计算，可知7次变换之后，四位数最后都会停在一个确定的数6174上．故答案为：7，6174
练习册系列答案
相关题目
的前
项和为
，且满足
．
，
，
，
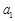的值并写出其通项公式；
）
)
)
所满足的等式是_________.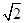
＝c＋d
，则三角形的面积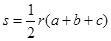
，根据类比思想，若四面体内切球半径为R，四个面的面积为S1、S2、S3、S4，则四面体的体积V= .
.
.
.
.
”，
的一次因式的积的形式）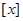
表示不超过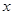
的最大整数，例如：
．
（ ）
，
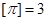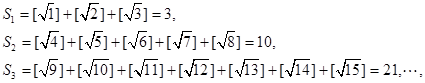
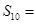(其中
), 则
，
，根据上面的结论，可以提出猜想: z1·z2·z3= ．